题目内容
几何模型:
条件:如下图,
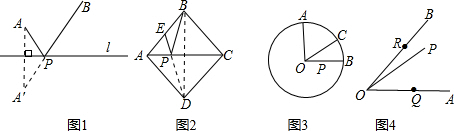
A、B是直线l同旁的两个定点.问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点
A关于直线l的对称点模型应用:
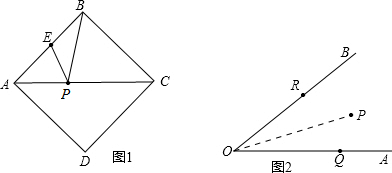
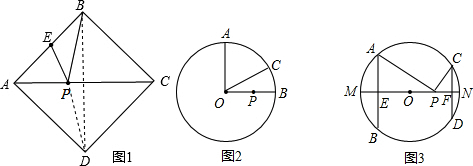
(1)如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连结BD,由正方形对称性可知,B与D关于直线AC对称.连结ED交AC于P,则PB+PE的最小值是________;

(2)如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则PA+PC的最小值是________;

(3)如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上
的动点,则△PQR周长的最小值是________.

答案:
解析:
解析:
|
(1) (2) (3) |

练习册系列答案
相关题目
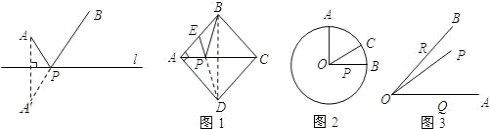
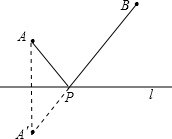 几何模型:条件:如图,A、B是直线l同旁的两个定点.
几何模型:条件:如图,A、B是直线l同旁的两个定点.