题目内容
 如图,六边形ABCDEF是⊙O的内接正六边形,若
如图,六边形ABCDEF是⊙O的内接正六边形,若 ,
, ,则向量
,则向量 可表示为
可表示为
- A.
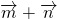
- B.
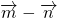
- C.

- D.

D
分析:首先根据圆的内接正六边形的性质,可求得:四边形OCDE是平行四边形,则可得: =
=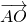 =-
=- =-
=- ,
,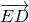 =
= =
= ,又由平行四边形法则,即可求得
,又由平行四边形法则,即可求得 的值.
的值.
解答: 解:连接OD,
解:连接OD,
∵六边形ABCDEF是⊙O的内接正六边形,
∴∠COD=∠OCD=∠ODC=∠ODE=∠OED=∠DOE=60°,
∴∠EOC=∠EDC=120°,
∴四边形OCDE是平行四边形,
∴OA=OD,OC=DE,
∴ =
=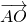 =-
=- =-
=- ,
,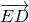 =
= =
= ,
,
∴ =
= +
+ =-
=- +(-
+(- )=-
)=- -
- .
.
故选D.
点评:此题考查了平面向量的知识,以及圆的内接正六边形的知识.注意平面向量是有方向性的,注意数形结合思想的应用.
分析:首先根据圆的内接正六边形的性质,可求得:四边形OCDE是平行四边形,则可得:
 =
=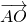 =-
=- =-
=- ,
,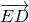 =
= =
= ,又由平行四边形法则,即可求得
,又由平行四边形法则,即可求得 的值.
的值.解答:
 解:连接OD,
解:连接OD,∵六边形ABCDEF是⊙O的内接正六边形,
∴∠COD=∠OCD=∠ODC=∠ODE=∠OED=∠DOE=60°,
∴∠EOC=∠EDC=120°,
∴四边形OCDE是平行四边形,
∴OA=OD,OC=DE,
∴
 =
=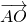 =-
=- =-
=- ,
,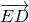 =
= =
= ,
,∴
 =
= +
+ =-
=- +(-
+(- )=-
)=- -
- .
.故选D.
点评:此题考查了平面向量的知识,以及圆的内接正六边形的知识.注意平面向量是有方向性的,注意数形结合思想的应用.

练习册系列答案
相关题目
 如图,四边形ABCD是由四个边长为l的正六边形所围住,则四边形ABCD的面积是( )
如图,四边形ABCD是由四个边长为l的正六边形所围住,则四边形ABCD的面积是( )A、
| ||||
B、
| ||||
| C、1 | ||||
| D、2 |


 如图,四边形ABCD的内角和为2×180°=360°,五边形ABCDE的内角和为3×180°=540°,…由此可见:
如图,四边形ABCD的内角和为2×180°=360°,五边形ABCDE的内角和为3×180°=540°,…由此可见:

