题目内容
已知抛物线:![]()
(1)求抛物线![]() 的顶点坐标.
的顶点坐标.
(2)将抛物线![]()
![]() 向右平移2个单位,再向上平移1个单位,得到抛物线
向右平移2个单位,再向上平移1个单位,得到抛物线![]() ,求抛物线
,求抛物线![]() 的解析式.
的解析式.
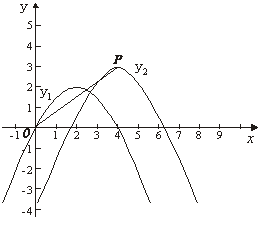
(3)如下图,抛物线![]() 的顶点为P,
的顶点为P,![]() 轴上有一动点M,在
轴上有一动点M,在![]() 、
、![]() 这两条抛物线上是否存在点N,使O(原点)、P、M、N四点构成以OP为一边的平行四边形,若存在,求出N点的坐标;若不存在,请说明理由.
这两条抛物线上是否存在点N,使O(原点)、P、M、N四点构成以OP为一边的平行四边形,若存在,求出N点的坐标;若不存在,请说明理由.
【提示:抛物线![]() (
(![]() ≠0)的对称轴是
≠0)的对称轴是![]() 顶点坐标是
顶点坐标是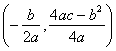 】
】
 |
解:(1)依题意 ![]() ………………………………………………1分
………………………………………………1分
∴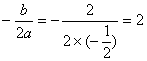 ,
, 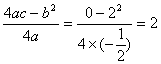 ………
………![]() …………………3分
…………………3分
∴顶点坐标是(2,2)……………………………………………………………4分
(2)根据题意可知
y2解析式中的二次项系数为![]() ……………………………………………………5分
……………………………………………………5分
且y2的顶点坐标是(4,3)…………………………………………………………6分
∴y2=-![]() ,即:y2=
,即:y2=![]() …………………………………8分
…………………………………8分
(3)符合条件的N点存在……………………………………………………………9分
如图:若四边形OPMN为符合条件的平行四边形,则![]() ∥
∥![]() ,且
,且![]()
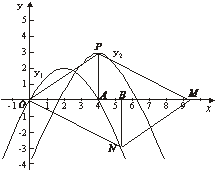 ∴
∴![]() ,
,
作![]() 轴于点A,
轴于点A,![]() 轴于点B
轴于点B
∴![]() ,
,
则有![]() (AAS) ∴
(AAS) ∴![]()
∵点P的坐标为(4,3)∴![]() ……10分
……10分
∵点N在抛物线![]() 、
、![]() 上,且P点为
上,且P点为
![]() 、
、![]() 的最高点 ∴符合条件的N点只能在
的最高点 ∴符合条件的N点只能在![]() 轴下方
轴下方
①点N在抛物线![]() 上,则有:
上,则有:![]()
解得:![]() 或
或![]() …………………………………………………11分
…………………………………………………11分
②点N在抛物线![]() 上,则有:
上,则有:![]()
解得:![]() 或
或![]() …………………13分
…………………13分
∴符合条件的N点有四个:
 ……………………………………………14分
……………………………………………14分

练习册系列答案
相关题目
 正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为
正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为 廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-
廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-