题目内容
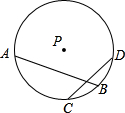如图，在圆O中，若AB与CD相交于点P，且PC=PD，PA=4，PB=1，则PC的长为________．
2
分析：由于弦AB、CD相交于点P，由相交弦定理知：PC•PD=PA•PB，然后代值计算，即可求得PC的长．
解答：由相交弦定理得：PA•PB=PC•PD，
已知PC=PD，则PC2=PA•PB=1×4=4，
故PC=2．
点评：此题主要考查的是相交弦定理的应用．
分析：由于弦AB、CD相交于点P，由相交弦定理知：PC•PD=PA•PB，然后代值计算，即可求得PC的长．
解答：由相交弦定理得：PA•PB=PC•PD，
已知PC=PD，则PC2=PA•PB=1×4=4，
故PC=2．
点评：此题主要考查的是相交弦定理的应用．
练习册系列答案
阅读快车系列答案
相关题目
24、如图，在圆O中，若AB与CD相交于点P，且PC=PD，PA=4，PB=1，则PC的长为
