题目内容
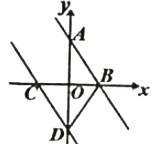
【题目】如图所示,∠AOB是平角,OM、ON分别是∠AOC、∠BOD的平分线.
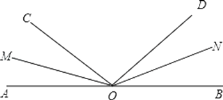
(1)当∠BOC=140°时,求∠AOM的度数;
(2)当∠AOC=30°,∠BOD=60°时,求∠MON的度数;
(3)当∠COD=x度时,则∠MON=________度.(请直接写出答案)
【答案】(1)20°;(2)135;(3)![]()
【解析】
(1)先求出∠AOC的度数,然后根据OM分别平分∠AOC即可求出∠AOM的度数;
(2)已知∠AOC、∠BOD度数且OM、ON分别平分∠AOC、∠BOD,可得∠AOM、∠BON度数,进而可得∠MON度数;
(3)由∠COD=α可知∠AOC+∠BOD=180°-α,根据角平分线可得∠AOC+∠BON=![]() (180°-α),进而可得∠MON.
(180°-α),进而可得∠MON.
(1) ∵∠AOB是平角,
∴∠AOC+∠COB=180°.
∵∠BOC=140°,
∴∠AOC=180°-140°=40°.
∵OM是∠AOC的平分线,
∴∠AOM=40°÷2=20°;
(2)∵∠AOB是平角,
∴∠AOB=180°.
∵OM、ON分别是∠AOC、∠BOD的平分线,
∴∠AOM=∠COM=∠AOC÷2, ∠BON=∠DON=∠BOD÷2,
∵∠AOC=30°,∠BOD=60°,
∴∠AOM=30°÷2=15°,∠BON=60°÷2=30°,
∴∠MON=180°-15°-30°=135°;
(3)∵OM、ON分别是∠AOC、∠BOD的角平分线,
∴∠AOM=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD,
∠BOD,
∴∠MON=180°-∠AOM-∠BON
=180°-![]() ∠AOC-
∠AOC-![]() ∠BOD
∠BOD
=180°-![]() (∠AOC+∠BOD)
(∠AOC+∠BOD)
=180°-![]() (180°-∠COD)
(180°-∠COD)
=90°+![]() x
x
=![]() 度.
度.

【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
小华根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … | -3 | -2 | -1 | 0 |
| 1 | 3 |
| 4 | 5 | 6 | 7 | … |
y | … |
|
|
|
|
| 6 | 6 |
|
|
|
| m | … |
求m的值;
(3)如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
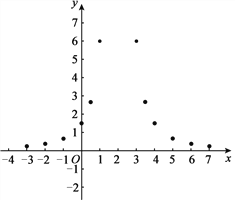
(4)结合函数的图象,写出该函数的一条性质: .