题目内容
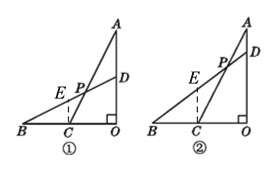
【题目】已知线段OA⊥OB,C为OB的中点,D为AO上一点,连接AC,BD交于点P.

(1)如图①,当OA=OB,且D为AO的中点时,求![]() 的值;
的值;
(2)如图②,当OA=OB,![]() =
=![]() 时,求tan ∠BPC的值.
时,求tan ∠BPC的值.
【答案】(1)2;(2)![]() .
.
【解析】试题分析:
(1)如图1,过点C作CE∥AO交BD于点E,由此可得△BCE∽△BOD,△CEP∽△ADP,从而可得:![]() ,
,![]() ,再由D是OA中点,可得:CE=
,再由D是OA中点,可得:CE=![]() OD=
OD=![]() AD,所以
AD,所以![]() =2;
=2;
(2)如图2,过点C作CE∥OA交BD于点E,设AD为![]() ,则由已知可得DO=3
,则由已知可得DO=3![]() ,AO=BO=
,AO=BO=![]() ,由勾股定理可得BD=
,由勾股定理可得BD=![]() ;由CE∥OA可得△BCE∽△BOD,△ECP∽△DAP,再由相似三角形的性质解得CE、DE,最后可得PD=
;由CE∥OA可得△BCE∽△BOD,△ECP∽△DAP,再由相似三角形的性质解得CE、DE,最后可得PD=![]() =AD,从而得到∠BPC=∠APD=∠A,就可在Rt△ACO中由求
=AD,从而得到∠BPC=∠APD=∠A,就可在Rt△ACO中由求![]() 来求
来求![]() 了.
了.
试题解析:
(1)过点C作CE∥OA 交BD于点E,
∴△BCE∽△BOD.
∵C为OB中点,D为AO中点,
∴CE=![]() OD=
OD=![]() AD.
AD.
∵CE∥AD,
∴△ECP∽△DAP,
∴![]() =
=![]() =2.
=2.
(2)过点C作CE∥OA交BD于点E.设AD=x,
∵OA=OB,![]() =
=![]() ,
,
∴AO=OB=4x,OD=3x.
∵CE∥OD,
∴△BCE∽△BOD,
∴CE=![]() OD=
OD=![]() x.
x.
∵CE∥AD,
∴△ECP∽△DAP,
∴![]() =
=![]() =
=![]() .由勾股定理可知BD=5x,则DE=
.由勾股定理可知BD=5x,则DE=![]() BD=
BD=![]() x.
x.
∴![]() =
=![]() =
=![]() =
=![]() ,解得PD=x,
,解得PD=x,
∴PD=AD.
∴∠BPC=∠DPA=∠A.
∵OA=OB,C是OB中点,
∴CO=![]() OB=
OB=![]() AO,
AO,
∴tan ∠BPC=tan A=![]() =
=![]() .
.

练习册系列答案
相关题目



