题目内容
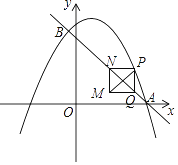
【题目】如图抛物线y=ax2+2交x轴于点A(﹣2,0)、B,交y轴于点C;
(1)求抛物线的解析式;
(2)点P从点A出发,以1个单位/秒的速度向终点B运动,同时点Q从点C出发,以相同的速度沿y轴正方向向上运动,运动的时间为t秒,当点P到达点B时,点Q也停止运动,设△PQC的面积为S,求S与t间的函数关系式并直接写出t的取值范围;
(3)在(2)的条件下,当点P在线段OB上时,设PQ交直线AC于点G,过P作PE⊥AC于点E,求EG的长.
【答案】(1)y=﹣![]() x2+2;(2)S=﹣
x2+2;(2)S=﹣![]() t2+t(0<t<2);S═
t2+t(0<t<2);S═![]() t2﹣t(2<t≤4);(3)
t2﹣t(2<t≤4);(3)![]() .
.
【解析】
(1)把A点坐标代入二次函数,解得a=-![]() ,即可求解;
,即可求解;
(2)利用S=![]() CQOP,分0<t<2、2<t≤4两种情况求解即可;
CQOP,分0<t<2、2<t≤4两种情况求解即可;
(3)过点G作GH⊥y轴,利用HG∥OP,得![]() =
=![]() ,求出GH=
,求出GH=![]() ,利用GE=EC+CG=即可求解.
,利用GE=EC+CG=即可求解.
解:(1)把A点坐标代入二次函数,解得a=﹣![]() ,
,
故:二次函数的表达式为:y=﹣![]() x2+2;
x2+2;
(2)S=![]() CQOP,
CQOP,
当0<t<2时,
S=![]() t(﹣t+2)=﹣
t(﹣t+2)=﹣![]() t2+t,
t2+t,
当2<t≤4时,
S═![]() t(t﹣2)=
t(t﹣2)=![]() t2﹣t;
t2﹣t;

(3)t秒时,AP=t,OP=t﹣2,CQ=t,
直线AC与x轴的夹角为45°,
则AE=![]() ,GC=
,GC=![]() GH,AC=2
GH,AC=2![]() ,HC=HG,
,HC=HG,
过点G作GH⊥y轴,交y轴于点H,
∵HG∥OP,
∴![]() =
=![]() ,
,
即:![]() =
=![]() ,
,
解得:GH=![]() ,
,
则:GC=![]() GH=
GH=![]()
GE=EC+CG=AC﹣AE+GC=2![]() ﹣
﹣![]() +
+![]()
![]() =
=![]() .
.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案【题目】九(1)班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”,“3”,“3”, “5”,“6”的四张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖,记每次抽出两张牌点数之差为x,按表格要求确定奖项.
奖项 | 一等奖 | 二等奖 | 三等奖 |
|x| | |x|=4 | |x|=3 | 1 |
(1)用列表或画树状图的方法求出甲同学获得一等奖的概率;
(2)求出每次抽奖获奖的概率?