Question

（1999•北京）如图所示，已知AB是⊙O中一条长为4的弦，P是⊙O上一动点，且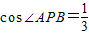，问是否存在以A、P、B为顶点的面积最大的三角形？试说明理由；若存在，求出这个三角形的面积．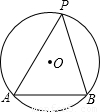

Answer 1

【答案】分析：由于AB的长固定，∠P的余弦值固定，则∠P的度数也就固定，当点P在AB的中垂线上时，AB边上的高是最大的，即，三角形的面积有最大值．根据余弦的概念和勾股定理求解即可．
解答：解：如图，PF是AB的中垂线，作BE⊥AP，垂足为E，
∵PB=PA，cos∠APB==，
∴PB=3PE，AE=2PE，
由勾股定理得，BE²=PB²-PE²=AB²-AE²，
∴9PE²-PE²=4²-4PE²，
故12PE²=16，
得PE=，AE=，PA=2，BE=，
∴S_△PAB=PA•BE=×2×=4．
点评：本题利用了中垂线的性质，余弦的概念，勾股定理和三角形的面积公式求解．