Question

【题目】如图，Rt△ABC中，∠BAC=90°，AB=2，AC=4，D是BC边上一动点，G是BC边上的一动点，GE∥AD分别交AC、BA或其延长线于F、E两点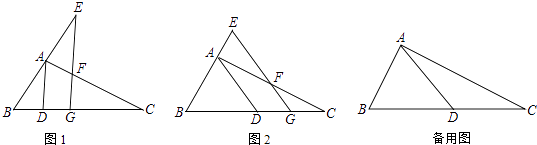

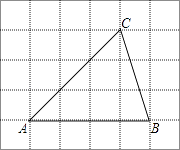
（1）如图1，当BC=5BD时，求证：EG⊥BC；
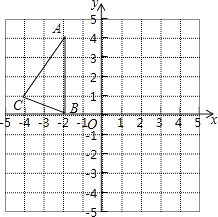
（2）如图2，当BD=CD时，FG+EG是否发生变化？证明你的结论；
（3）当BD=CD，FG=2EF时，DG的值= ．

Answer 1

【答案】
（1）

证明：如图1，

∵∠BAC=90°，AB=2，AC=4，

∴BC=2 ，

∵BC=5BD，

∴BD= ，

∴ = =

又∵∠DBA=∠ABC，

∴△BDA∽△BAC，

∴∠BDA=∠BAC=90°，

∵EG∥AD，

∴EG⊥BC．

（2）

证明：FG=EG=2 不变，

证法1：如图2，

∵EG∥AD，

∴△CFG∽△CAD，

∴ = ，

同理 = ，

∵BD=CD，

∴ + = + =2，

∴EG+FG=2AD，

∵BD=CD，∠BAC=90°，

∴AD= BC= ，

∴EG+FG=2AD=2 ．

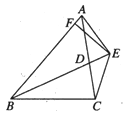
证法2：如图3，

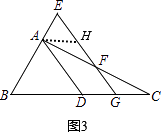
取EF的中点，易证四边形ADGH是平行四边形，

得出EG+FG=2GH=2AD=2 ．

证法3：如图4，

中线AD加倍到M，易证四边形AMNE是平行四边形，

得出EG+FG=EN=AM=2AD=2 ．

（3）
或
【解析】（3）如图5，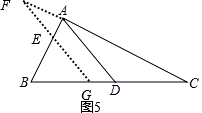

当BD=CD，FG=2EF时，
则GE=EF，
∵GE∥AD，AD∥GF，
∴△CFG∽△CAD，△ABD∽△BGE，
∴ = ， = ，
∴ = = ；
又BG+CG=2 ，
∴BG= ，
∴DG=BD=BG= ；
如图6，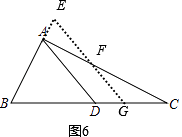

当BD=CD，FG=2EF时，
则GE=EF，
∵GE∥AD，AD∥GF，
∴△CFG∽△CAD，△ABD∽△AGE，
∴ = ， = ，
∴ = = ；
又BG+CG=2 ，
∴CG= ，
∴DG=CD﹣CG= ．
综上所知DG为 或 ．
【考点精析】利用勾股定理的概念对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．