题目内容
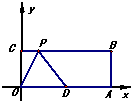 12、已知:如图,在直角坐标系中,O为坐标原点,四边形OABC为矩形,A、C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为
12、已知:如图,在直角坐标系中,O为坐标原点,四边形OABC为矩形,A、C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为
P(3,4)P(2,4)P(8,4)
.分析:题中没有指明△ODP的腰长与底分别是哪个边,故应该分情况进行分析,从而求得点P的坐标.
解答:解:分情况讨论:
①当OD是等腰三角形的底边时,P就是OD的垂直平分线与CB的交点,此时OP=PD≠5;
②当OD是等腰三角形的一条腰时:若点O是顶角顶点时,P点就是以点O为圆心,以5为半径的弧与CB的交点,根据勾股定理可得P的坐标是(3,4).
若D是顶角顶点时,P点就是以点D为圆心,以5为半径的弧与CB的交点,根据勾股定理可得P的坐标是(2,4)或(8,4).
故答案为:(3,4)或(2,4)或(8,4).
①当OD是等腰三角形的底边时,P就是OD的垂直平分线与CB的交点,此时OP=PD≠5;
②当OD是等腰三角形的一条腰时:若点O是顶角顶点时,P点就是以点O为圆心,以5为半径的弧与CB的交点,根据勾股定理可得P的坐标是(3,4).
若D是顶角顶点时,P点就是以点D为圆心,以5为半径的弧与CB的交点,根据勾股定理可得P的坐标是(2,4)或(8,4).
故答案为:(3,4)或(2,4)或(8,4).
点评:此题主要考查等腰三角形的性质及勾股定理的运用,注意正确的进行分类,考虑到所有的可能情况是解题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目

 的图象的一个分支位于第一象限.
的图象的一个分支位于第一象限.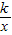 的图象的图象上,求k的值;
的图象的图象上,求k的值; S1?
S1?
 的图象与y轴交于点A,
的图象与y轴交于点A, 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐 时x的取值范围。
时x的取值范围。
 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
