题目内容
证明题：在△ABC中，AB＞AC，AD是中线，AE是高，求证：AB2-AC2=2BC•DE．
分析：由勾股定理可得出AB2=BE2+AE2，AC2=AE2+EC2，则AB2-AC2=BE2-EC2，由平方差公式可得出答案．
解答：解：∵AE是高，
∴△ABE和△ACE是直角三角形，
∴AB2=BE2+AE2，AC2=AE2+EC2，
∴AB2-AC2=BE2-EC2
=（BE+CE）（BE-CE）
=BC（BD+DE-CE），
∵AD是中线，
∴AB2-AC2=BC（CD+DE-CE）
=BC（DE+DE）
=2BC•DE．
∴△ABE和△ACE是直角三角形，
∴AB2=BE2+AE2，AC2=AE2+EC2，
∴AB2-AC2=BE2-EC2
=（BE+CE）（BE-CE）
=BC（BD+DE-CE），
∵AD是中线，
∴AB2-AC2=BC（CD+DE-CE）
=BC（DE+DE）
=2BC•DE．
点评：本题考查了勾股定理以及三角形的角平分线、中线和高线，是基础知识要熟练掌握．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
辨析题：在△ABC中，已知AB＞AC，求证：AB=AC．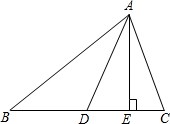
证明题：
辨析题：在△ABC中，已知AB＞AC，求证：AB=AC．