题目内容
如图,在平面直角坐标系中,△ABC的边AB在x轴上,∠ABC=90°,AB=BC,OA=1,OB=4,抛物
线 经过A、C两点.
经过A、C两点.
(1)求抛物线的解析式及其顶点坐标;
(2)如图①,点P是抛物线上位于x轴下方的一点,点Q与点P关于抛物线的对称轴对称,过点P、Q分别向x轴作垂线,垂足为点D、E,记矩形DPQE的周长为d,求d的最大值,并求出使d最大值时点P的坐标;
(3)如图②,点M是抛物线上位于直线AC下方的一点,过点M作MF⊥AC于点F,连接MC,作MN∥BC交直线AC于点N,若MN将△MFC的面积分成2:3两部分,请确定M点的坐标.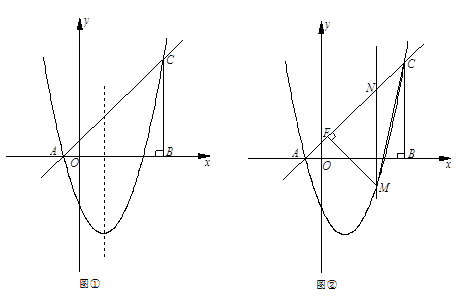
(1)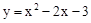 ,(1,
,(1,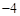 );(2)(0,
);(2)(0,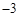 )或(2,
)或(2,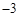 );(3)
);(3)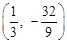 或
或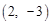 .
.
解析试题分析:(1)根据曲线上点的坐标与方程的关系,将A(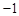 ,0)C(4,5)代入
,0)C(4,5)代入 得方程组,解之即可得抛物线的解析式;化为顶点式即可得顶点坐标.
得方程组,解之即可得抛物线的解析式;化为顶点式即可得顶点坐标.
(2)点P为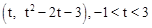 ,分
,分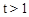 和
和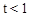 ,把矩形DPQE的周长表示为
,把矩形DPQE的周长表示为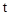 的二次函数,应用二次函数最值原理求解即可.
的二次函数,应用二次函数最值原理求解即可.
(3)分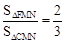 和
和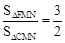 两种情况讨论即可.
两种情况讨论即可.
(1)由已知得:A(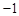 ,0)、C(4,5),
,0)、C(4,5),
∵二次函数 的图像经过点A(-1,0)C(4,5),
的图像经过点A(-1,0)C(4,5),
∴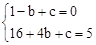 , 解得
, 解得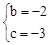 .
.
∴抛物线解析式为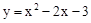 .
.
∵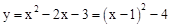 ,∴顶点坐标为(1,
,∴顶点坐标为(1,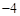 ).
).
(2)如答图①,由(1)知抛物线的对称轴为直线x=1,
设点P为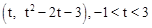 ,
,
∵P、Q为抛物线上的对称点,∴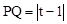 .
.
当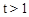 时,
时,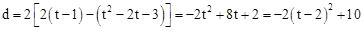 ,
,
∵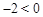 ,∴当t=2使,d有最大值为10,即点P为(2,
,∴当t=2使,d有最大值为10,即点P为(2,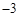 )
)
当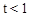 时,由抛物线的轴对称性得,点P为(0,
时,由抛物线的轴对称性得,点P为(0,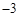 )时,d有最大值10
)时,d有最大值10
综上所述,当P为(0,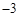 )或(2,
)或(2,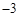 )时,d有最大值10
)时,d有最大值10
(3)如答图②,过点F作FH⊥MN于H,过C作CG⊥MN于G,则∠ANM=∠ACB=45°.
∵MF⊥AC,∴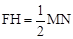 . ∴
. ∴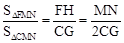 .
.
∵A(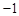 ,0),C(4,5),∴直线AC解析式为y=x+1.
,0),C(4,5),∴直线AC解析式为y=x+1.
设点M为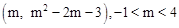 ,则CG=4-m.
,则CG=4-m.
由MN∥BC得点N为(m,m+1),
∴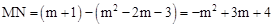 .
.
当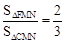 时,有3MN="4CG" ,即
时,有3MN="4CG" ,即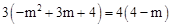 ,
,
解得: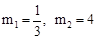 (舍去).
(舍去).
∴点M为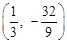 .
.
当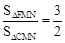 时,有MN=3CG, 即
时,有MN=3CG, 即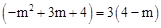 ,
,
解得: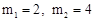 (舍去).
(舍去).
∴点M为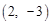 .
.
综上所述,当M为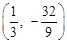 或
或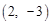 时,MN将△MFC的面积分成2:3两部分.
时,MN将△MFC的面积分成2:3两部分. 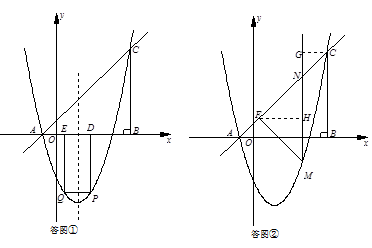
考点:1.二次函数综合题;2.曲线上点的坐标与方程的关系;3.二次函数的性质;4.解一元二次方程;5.分类思想的应用.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案 与
与 轴交于
轴交于 两点,与
两点,与 轴交于点
轴交于点 ,连结AC,若
,连结AC,若
 时,求出点
时,求出点 的坐标;
的坐标; ,
, 是线段
是线段 、
、 重合)的一个动点.过点
重合)的一个动点.过点 ,交抛物线于点
,交抛物线于点 ,连结
,连结 、
、 ,设点
,设点 的面积最大?最大面积为多少?
的面积最大?最大面积为多少?
 )秒.
)秒.
 ,
, 求该抛物线与x轴的交点坐标;
求该抛物线与x轴的交点坐标; ,证明抛物线与x轴有两个交点;
,证明抛物线与x轴有两个交点; 且抛物线在
且抛物线在 区间上的最小值是-3,求b的值.
区间上的最小值是-3,求b的值. 经过点A(6,0),且顶点B(m,6)在直线
经过点A(6,0),且顶点B(m,6)在直线 上.
上. ,在x轴上有一点D(10,0),连接DC,且直线DC与y轴交于点E.
,在x轴上有一点D(10,0),连接DC,且直线DC与y轴交于点E.

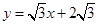 与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8
与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8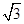 ,抛物线经过等腰梯形的四个顶点.
,抛物线经过等腰梯形的四个顶点.
 轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
 x2+
x2+ x(0≤x≤10).发射3 s后,导弹到达A点,此时位于与L同一水面的R处雷达站测得AR的距离是2 km,再过3 s后,导弹到达B点.
x(0≤x≤10).发射3 s后,导弹到达A点,此时位于与L同一水面的R处雷达站测得AR的距离是2 km,再过3 s后,导弹到达B点.
