题目内容
我们已经学过直角三角形的一个重要性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.小明得出,如图△ABC中,有∠B=60°,2BC=AB.爱动脑筋的他想,如果先画∠ABC=60°,且有2BC=AB,比如 ,BC=1,AB=2,连接AC,那么得到的△ABC是否是直角三角形呢?画完后他发现是的,你能帮他证明吗?
,BC=1,AB=2,连接AC,那么得到的△ABC是否是直角三角形呢?画完后他发现是的,你能帮他证明吗?
 解:作AB边上的中线CD.
解:作AB边上的中线CD.∵BC=
 AB,
AB,∴BC=BD,
又∵∠B=60°,
∴△BCD为正是三角形.
∠3=∠4=60°,
又∵AD=BD,AD=CD,
∴∠1=∠2=
 ∠3=
∠3= ×60°=30°,
×60°=30°,∴∠2+∠4=30°+60°=90°,
∴△ABC是直角三角形.
分析:作出AB边上的中线CD,根据等边三角形的判定可知△CDB为等边三角形,再根据三角形内角和外角的关系求出∠ACD的度数为30°,然后计算出∠ACB为90°即可.
点评:此题考查了等腰三角形的性质、等边三角形的性质及判定、直角三角形的判定.作出CD边上的中线是解题的关键.

练习册系列答案
相关题目

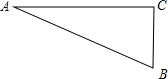 ,BC=1,AB=2,连接AC,那么得到的△ABC是否是直角三角形呢?画完后他发现是的,你能帮他证明吗?
,BC=1,AB=2,连接AC,那么得到的△ABC是否是直角三角形呢?画完后他发现是的,你能帮他证明吗?
