题目内容
【题目】如图,![]() 中,
中,![]() ,
,![]() .
.![]() ,点
,点![]() 是
是![]() 上一点,以
上一点,以![]() 为圆心作
为圆心作![]() ,
,
![]() 若
若![]() 经过
经过![]() 、
、![]() 两点,求
两点,求![]() 的半径,并判断点
的半径,并判断点![]() 与
与![]() 的位置关系.
的位置关系.
![]() 若
若![]() 和
和![]() 、
、![]() 都相切,求
都相切,求![]() 的半径.
的半径.

【答案】![]() 的半径为
的半径为![]() ,点
,点![]() 在
在![]() 上
上![]() 的半径为
的半径为![]()
【解析】
(1)设点D是AC的中点,连接CM,DM,易得CM=AM=BM,继而求得⊙M的半径,并判断点B与⊙M的位置关系.
(2)首先连接EM,FM,可得四边形CEMF是正方形,设EM=x,则CE=x,由△AEM∽△ACB,根据相似三角形的对应边成比例求得答案.
![]() ∵
∵![]() 经过
经过![]() 、
、![]() 两点,
两点,
∴![]() 在
在![]() 的垂直平分线上,
的垂直平分线上,
设点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
连接![]() ,
,
∵![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的半径为
的半径为![]() ,点
,点![]() 在
在![]() 上.
上.
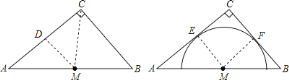
![]() 连接
连接![]() ,
,![]() ,
,
∵![]() 和
和![]() 、
、![]() 都相切,
都相切,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴四边形![]() 是正方形,
是正方形,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:![]() .
.
即![]() 的半径为
的半径为![]() .
.

练习册系列答案
相关题目