题目内容
若0<a<1,则a,(-a)2,| 1 | a |
分析:由于0<a<1,利用不等式性质,可得0<a2<a,即a2<a<1,根据a<1,利用不等式性质还可得出1<
,又a2=(-a)2于是有(-a)2<a<
.
| 1 |
| a |
| 1 |
| a |
解答:解:∵0<a<1,
∴0<a2<a,
∴a2<a<1,
又∵(-a)2=a2,
∴(-a)2<a<1,
∵a<1,
∴1<
,
∴(-a)2<a<
.
故答案为:(-a)2<a<
.
∴0<a2<a,
∴a2<a<1,
又∵(-a)2=a2,
∴(-a)2<a<1,
∵a<1,
∴1<
| 1 |
| a |
∴(-a)2<a<
| 1 |
| a |
故答案为:(-a)2<a<
| 1 |
| a |
点评:本题主要利用了不等式的性质,在不等式的两边同乘以不等于0的数,不等式的方向不变.

练习册系列答案
相关题目

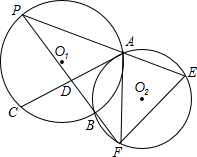 、PB的延长线分别交⊙O2于点E、F,PB交AC于D.
、PB的延长线分别交⊙O2于点E、F,PB交AC于D. 已知△ABC中,D是AB上一点,∠BCD=∠A,若BD=1,AD=2,则BC=
已知△ABC中,D是AB上一点,∠BCD=∠A,若BD=1,AD=2,则BC=