题目内容
【题目】在平面直角坐标系xOy中,点C坐标为(6,0),以原点O为顶点的四边形OABC是平行四边形,将边OA沿x轴翻折得到线段![]() ,连接
,连接![]() 交线段OC于点D.
交线段OC于点D.
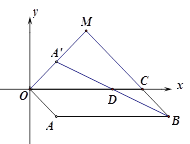
(1)如图1,当点A在y轴上,且A(0,-2)时.
① 求![]() 所在直线的函数表达式;
所在直线的函数表达式;
② 求证:点D为线段![]() 的中点.
的中点.
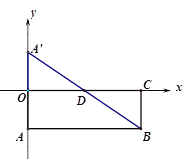
(2)如图2,当![]() 时,
时, ![]() ,BC的延长线相交于点M,试探究
,BC的延长线相交于点M,试探究![]() 的值,并写出探究思路.
的值,并写出探究思路.
【答案】(1)①![]() ,②见解析;(2)
,②见解析;(2) ![]()
【解析】试题分析:(1)① 先求点A、B的坐标,再根据对称求得![]() 的坐标,再用待定系数法求直线
的坐标,再用待定系数法求直线![]() B的解析式;②根据ASA证明△
B的解析式;②根据ASA证明△![]() ≌△BDC,再得出
≌△BDC,再得出![]() =BD,即点D是
=BD,即点D是![]() 的中点;(2)连接
的中点;(2)连接![]() 交x轴于F点,先证明F为
交x轴于F点,先证明F为![]() 的中点,得出点D为线段
的中点,得出点D为线段![]() 的中点,由边OA沿x轴翻折得到线段
的中点,由边OA沿x轴翻折得到线段![]() 且
且 ![]() ,得出
,得出![]() ,
, ![]() ,又由AO∥BC得出
,又由AO∥BC得出![]() ,过点D作DE∥BM交OM于点E ,可得
,过点D作DE∥BM交OM于点E ,可得![]() ,所以
,所以![]() ,再得到
,再得到![]() . .
. .
试题解析:
(1)①四边形OABC是平行四边形
∴AO∥BC,AO=BC .
又∵点A落在y轴上,
∴AO⊥x轴,
∴BC⊥x轴.
∵A(0,-2)C(6,0),
∴B(6,-2).
又∵边OA沿x轴翻折得到线段![]() ,
,
∴![]() (0,2).
(0,2).
设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
![]()
解得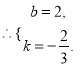
∴![]() 所在直线的函数表达式为
所在直线的函数表达式为![]() .
.
证明:②∵四边形OABC是平行四边形,
∴AO∥BC,AO=BC .
∴∠![]() =∠DBC.
=∠DBC.
又∵边OA沿x轴翻折得到线段![]() ,
,
∴AO= ![]() .
.
∴![]() =BC.
=BC.
又∵∠![]() =∠BDC,
=∠BDC,
∴△![]() ≌△BDC
≌△BDC
∴![]() =BD,
=BD,
∴点D为线段![]() 的中点.
的中点.
(2)![]()
理由:连接![]() 交x轴于F点
交x轴于F点
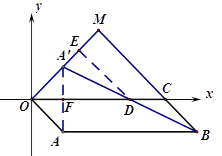
证明F为![]() 的中点;
的中点;
∴ 得出点D为线段![]() 的中点
的中点
∵边OA沿x轴翻折得到线段![]() 且
且 ![]() ,
,
∴![]() ,
, ![]() .
.
∵AO∥BC,
∴![]() .
.
过点D作DE∥BM交OM于点E ,
可得![]() ,
,
还可得到等腰直角△![]() .
.
∴![]() .
.
∴![]() .
.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目

