题目内容
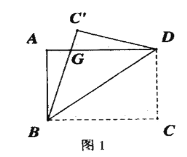
【题目】如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于
轴交于![]() .
.
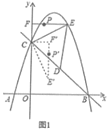
(1)求函数表达式;
(2)点![]() 是线段
是线段![]() 中点,点
中点,点![]() 是
是![]() 上方抛物线上一动点,连接
上方抛物线上一动点,连接![]() ,
,![]() .当
.当![]() 的面积最大时,过点
的面积最大时,过点![]() 作
作![]() 轴垂线,垂足为
轴垂线,垂足为![]() ,点
,点![]() 为线段
为线段![]() 上一动点,将
上一动点,将![]() 绕点
绕点![]() 顺时针方向旋转90°,点
顺时针方向旋转90°,点![]() ,
,![]() ,
,![]() 的对应点分别是
的对应点分别是![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,先沿适当的路径运动到点
出发,先沿适当的路径运动到点![]() 处,再沿
处,再沿![]() 运动到点
运动到点![]() 处,最后沿适当的路径运动到点
处,最后沿适当的路径运动到点![]() 处停止.求
处停止.求![]() 面积的最大值及点
面积的最大值及点![]() 经过的最短路径的长;
经过的最短路径的长;
【答案】(1)![]() ;(2)最大面积为
;(2)最大面积为![]() ;点Q运动最短路径为
;点Q运动最短路径为![]()
【解析】
(1)根据题意可设二次函数顶点式,再用待定系数法求解即可.
(2)观察图形发现![]() 本身的面积不易表示,由条件点
本身的面积不易表示,由条件点![]() 是线段
是线段![]() 中点想到三角形的中线将其面积分为相等的两部分,所以将求
中点想到三角形的中线将其面积分为相等的两部分,所以将求![]() 面积最大值转化为求
面积最大值转化为求 ![]() 的面积最大值,方法可过
的面积最大值,方法可过![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 于点
于点![]() ,通过二次函数解析式与直线
,通过二次函数解析式与直线![]() 的解析式分别设出点
的解析式分别设出点![]() 与点
与点![]() 的坐标,再表示出
的坐标,再表示出![]() 的面积转化为新的二次函数求最值;
的面积转化为新的二次函数求最值;
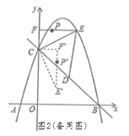
求点![]() 经过的最短路径,先要确定点
经过的最短路径,先要确定点![]() 的位置,可作点
的位置,可作点![]() 关于
关于![]() 的对称点
的对称点![]() ,连接
,连接![]() 交
交![]() 于一点,该点即为点
于一点,该点即为点![]() 运动路径最短时的点
运动路径最短时的点![]() ,原因是此时
,原因是此时![]() 与
与![]() 共线,最后根据点的坐标求出线段长度即可.
共线,最后根据点的坐标求出线段长度即可.
因为抛物线与![]() 轴交于
轴交于![]() ,
,![]() 两点,
两点,
可设函数解析式为:![]() ,
,
根据题意得:![]()
解得:![]()
∴解析式为:![]() ;
;
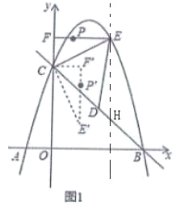
(2)∵点![]() 是线段
是线段![]() 中点
中点
∴![]()
∴当![]() 面积最大时,
面积最大时,![]() 的面积最大;
的面积最大;
过![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 于点
于点![]() ,
,
易得直线![]() 的直线方程为:
的直线方程为:![]()
设![]() ,
,![]()
∴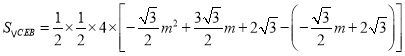
![]()
当![]() 时,
时,![]() 有最大面积,最大面积为
有最大面积,最大面积为![]()
∴![]() ,
,![]() ,
,
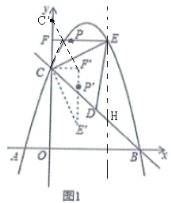
作点![]() 关于
关于![]() 的对称点
的对称点![]() ,
,
连接![]() 交
交![]() 于一点,该点即为点
于一点,该点即为点![]() 运动路径最短时的点
运动路径最短时的点![]() ,
,
因为![]() ,
, ![]() ,所以
,所以![]()
根据旋转的性质,![]() ,所以
,所以![]()
因为![]() 与
与![]() 关于
关于![]() 对称,所以
对称,所以![]()
∴在![]() 中,
中,![]()
∴点![]() 运动最短路径为
运动最短路径为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目