题目内容
我市的公租房建设卓有成效，目前已有部分公租房投入使用，计划从今年起，在未来的10年内解决低收入人群的住房问题，预计第x年竣工并投入使用的公租房面积y（百万平方米）满足这样的关系式：1≤x≤6时，
；7≤x≤10时，
．同时，政府每年将向租户收取一定的租金，假设每年的公租房全部出租完，另外随着物价上涨等因素的影响，每年的租金也会随之上调，预测：第x年竣工并投入使用的公租房租金z（元/m2）与时间x（年）满足以下表：| z（元/m2） | 50 | 52 | 54 | 56 | … |
| x（年） | 1 | 2 | 3 | 4 | … |
（2）求政府在哪一年竣工并投入使用的公租房收取的租金最多，最多是多少？
（3）若第6年竣工投入使用的公租房可解决20万人的住房问题，政府计划在第10年竣工投入使用的公租房在原预计总面积不变的情况下，要让人均住房面积比第6年提高a%，这样解决住房的人数将比第6年解决的人数减少1.35a%，求a的值（结果保留整数）．（参考数据：172=289，182=324，192=361）
【答案】分析：（1）由自变量x逐渐增大，而相对应的函数值z逐渐增大，且数据均匀增加，可以推测z是x的一次函数；
（2）利用公租房收取的租金=公租房租金z（元/m2）×投入使用的公租房面积y（百万平方米）列出二次函数，利用配方法求得最大值即可；
（3）利用第6年人均住房面积×（1+a%）×第6年解决的人数×（1-1.35a%）=第10年人均住房面积，列方程解决问题．
解答：解：（1）估计z是x的一次函数．
设z=kx+b，把（1，50）（2，52）代入函数解析式解得k=2，b=48，
所以z=48+2x；
（2）设第x年竣工并投入使用的公租房收取的租金为w百万元w=y•z，
当1≤x≤6时：
=
=-
（x-3）2+243，
x=3时，Wmax=243（百万元）；
当7≤x≤10时，
=
=-
（x-7）2+
，
；
∵243＞
，
∴第3年时，收取的租金最多，最多是243百万元；
（3）∵第6年人均住房面积是（-
×6+5）×100÷20=20，
∴20×（1+a%）×20×（1-1.35a%）=（-
×10+
）×100，
设a%=x，
解得：x1≈0.2，x2=
＜0（舍去），
∴a=20．
点评：此题综合考查了待定系数法求一次函数，利用配方法求二次函数的最值以及利用基本数量关系建立方程解决实际问题，是一道比较好的题目．
（2）利用公租房收取的租金=公租房租金z（元/m2）×投入使用的公租房面积y（百万平方米）列出二次函数，利用配方法求得最大值即可；
（3）利用第6年人均住房面积×（1+a%）×第6年解决的人数×（1-1.35a%）=第10年人均住房面积，列方程解决问题．
解答：解：（1）估计z是x的一次函数．
设z=kx+b，把（1，50）（2，52）代入函数解析式解得k=2，b=48，
所以z=48+2x；
（2）设第x年竣工并投入使用的公租房收取的租金为w百万元w=y•z，
当1≤x≤6时：
==-（x-3）2+243，x=3时，Wmax=243（百万元）；
当7≤x≤10时，
==-（x-7）2+，；∵243＞
，∴第3年时，收取的租金最多，最多是243百万元；
（3）∵第6年人均住房面积是（-
×6+5）×100÷20=20，∴20×（1+a%）×20×（1-1.35a%）=（-
×10+）×100，设a%=x，
解得：x1≈0.2，x2=
＜0（舍去），∴a=20．
点评：此题综合考查了待定系数法求一次函数，利用配方法求二次函数的最值以及利用基本数量关系建立方程解决实际问题，是一道比较好的题目．
练习册系列答案
相关题目
我市的公租房建设卓有成效，目前已有部分公租房投入使用，计划从今年起，在未来的10年内解决低收入人群的住房问题，预计第x年竣工并投入使用的公租房面积y（百万平方米）满足这样的关系式：1≤x≤6时，y=-
x+5；7≤x≤10时，y=-
x+
．同时，政府每年将向租户收取一定的租金，假设每年的公租房全部出租完，另外随着物价上涨等因素的影响，每年的租金也会随之上调，预测：第x年竣工并投入使用的公租房租金z（元/m2）与时间x（年）满足以下表：
（1）试估计z与x之间的函数类型，并求出该函数表达式；
（2）求政府在哪一年竣工并投入使用的公租房收取的租金最多，最多是多少？
（3）若第6年竣工投入使用的公租房可解决20万人的住房问题，政府计划在第10年竣工投入使用的公租房在原预计总面积不变的情况下，要让人均住房面积比第6年提高a%，这样解决住房的人数将比第6年解决的人数减少1.35a%，求a的值（结果保留整数）．（参考数据：172=289，182=324，192=361）
| 1 |
| 6 |
| 1 |
| 8 |
| 19 |
| 4 |
| z（元/m2） | 50 | 52 | 54 | 56 | … |
| x（年） | 1 | 2 | 3 | 4 | … |
（2）求政府在哪一年竣工并投入使用的公租房收取的租金最多，最多是多少？
（3）若第6年竣工投入使用的公租房可解决20万人的住房问题，政府计划在第10年竣工投入使用的公租房在原预计总面积不变的情况下，要让人均住房面积比第6年提高a%，这样解决住房的人数将比第6年解决的人数减少1.35a%，求a的值（结果保留整数）．（参考数据：172=289，182=324，192=361）
我市的公租房建设卓有成效，目前已有部分公租房投入使用，计划从今年起，在未来的10年内解决低收入人群的住房问题，预计第x年竣工并投入使用的公租房面积y（百万平方米）满足这样的关系式：1≤x≤6时，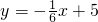
；7≤x≤10时，
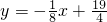．同时，政府每年将向租户收取一定的租金，假设每年的公租房全部出租完，另外随着物价上涨等因素的影响，每年的租金也会随之上调，预测：第x年竣工并投入使用的公租房租金z（元/m2）与时间x（年）满足以下表：
| z（元/m2） | 50 | 52 | 54 | 56 | … |
| x（年） | 1 | 2 | 3 | 4 | … |
（2）求政府在哪一年竣工并投入使用的公租房收取的租金最多，最多是多少？
（3）若第6年竣工投入使用的公租房可解决20万人的住房问题，政府计划在第10年竣工投入使用的公租房在原预计总面积不变的情况下，要让人均住房面积比第6年提高a%，这样解决住房的人数将比第6年解决的人数减少1.35a%，求a的值（结果保留整数）．（参考数据：172=289，182=324，192=361）
我市的公租房建设卓有成效，目前已有部分公租房投入使用，计划从今年起，在未来的10年内解决低收入人群的住房问题，预计第x年竣工并投入使用的公租房面积y（百万平方米）满足这样的关系式：1≤x≤6时，
；7≤x≤10时，
．同时，政府每年将向租户收取一定的租金，假设每年的公租房全部出租完，另外随着物价上涨等因素的影响，每年的租金也会随之上调，预测：第x年竣工并投入使用的公租房租金z（元/m2）与时间x（年）满足以下表：
（1）试估计z与x之间的函数类型，并求出该函数表达式；
（2）求政府在哪一年竣工并投入使用的公租房收取的租金最多，最多是多少？
（3）若第6年竣工投入使用的公租房可解决20万人的住房问题，政府计划在第10年竣工投入使用的公租房在原预计总面积不变的情况下，要让人均住房面积比第6年提高a%，这样解决住房的人数将比第6年解决的人数减少1.35a%，求a的值（结果保留整数）．（参考数据：172=289，182=324，192=361）
；7≤x≤10时，．同时，政府每年将向租户收取一定的租金，假设每年的公租房全部出租完，另外随着物价上涨等因素的影响，每年的租金也会随之上调，预测：第x年竣工并投入使用的公租房租金z（元/m2）与时间x（年）满足以下表：| z（元/m2） | 50 | 52 | 54 | 56 | … |
| x（年） | 1 | 2 | 3 | 4 | … |
（2）求政府在哪一年竣工并投入使用的公租房收取的租金最多，最多是多少？
（3）若第6年竣工投入使用的公租房可解决20万人的住房问题，政府计划在第10年竣工投入使用的公租房在原预计总面积不变的情况下，要让人均住房面积比第6年提高a%，这样解决住房的人数将比第6年解决的人数减少1.35a%，求a的值（结果保留整数）．（参考数据：172=289，182=324，192=361）
我市的公租房建设卓有成效，目前已有部分公租房投入使用，计划从今年起，在未来的10年内解决低收入人群的住房问题，预计第x年竣工并投入使用的公租房面积y（百万平方米）满足这样的关系式：1≤x≤6时，
；7≤x≤10时，
．同时，政府每年将向租户收取一定的租金，假设每年的公租房全部出租完，另外随着物价上涨等因素的影响，每年的租金也会随之上调，预测：第x年竣工并投入使用的公租房租金z（元/m2）与时间x（年）满足以下表：
（1）试估计z与x之间的函数类型，并求出该函数表达式；
（2）求政府在哪一年竣工并投入使用的公租房收取的租金最多，最多是多少？
（3）若第6年竣工投入使用的公租房可解决20万人的住房问题，政府计划在第10年竣工投入使用的公租房在原预计总面积不变的情况下，要让人均住房面积比第6年提高a%，这样解决住房的人数将比第6年解决的人数减少1.35a%，求a的值（结果保留整数）．（参考数据：172=289，182=324，192=361）
；7≤x≤10时，．同时，政府每年将向租户收取一定的租金，假设每年的公租房全部出租完，另外随着物价上涨等因素的影响，每年的租金也会随之上调，预测：第x年竣工并投入使用的公租房租金z（元/m2）与时间x（年）满足以下表：| z（元/m2） | 50 | 52 | 54 | 56 | … |
| x（年） | 1 | 2 | 3 | 4 | … |
（2）求政府在哪一年竣工并投入使用的公租房收取的租金最多，最多是多少？
（3）若第6年竣工投入使用的公租房可解决20万人的住房问题，政府计划在第10年竣工投入使用的公租房在原预计总面积不变的情况下，要让人均住房面积比第6年提高a%，这样解决住房的人数将比第6年解决的人数减少1.35a%，求a的值（结果保留整数）．（参考数据：172=289，182=324，192=361）