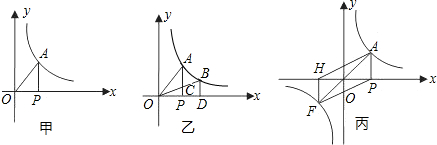
题目内容
(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE=10, 求直角梯形ABCD的面积.
设梯形OPFE的面积为S.
(1) A(20,0),B(0,20) ∴OA=OB=20,∠A=∠B=45°..
当t=1时,OE=1,AP=3,∴OP=17,EF=BE=19.
∴S=![]() (OP+EF)·OE=18.
(OP+EF)·OE=18.
 (2) OE=t,AP=3t,∴OP=20-3t,EF=BE=20-t.
(2) OE=t,AP=3t,∴OP=20-3t,EF=BE=20-t.
∴S=![]() (OP+EF)·OE=
(OP+EF)·OE=![]() (20-3t +20-t)·t =-2t2+20t=-2(t-5)2+50.
(20-3t +20-t)·t =-2t2+20t=-2(t-5)2+50.
∴当t=5 (在0<t<![]() 范围内)时,S最大值=50.
范围内)时,S最大值=50.

当t=t1时,AF1=![]() t1,AP1=3t1;当t=t2时,AF2=
t1,AP1=3t1;当t=t2时,AF2=![]() t2,AP2=3t2;
t2,AP2=3t2;
∴![]() ,又∠A=∠A,∴△AF1P1∽
,又∠A=∠A,∴△AF1P1∽![]() △AF2P2.
△AF2P2.

练习册系列答案
相关题目