题目内容
如图，梯形ABCD纸片，AD∥BC，现将纸片沿EF折叠，使点C与点A重合，点D落在点G处，展开后，若∠AFG=30°，则∠CEF=________°．
75
分析：连CF，根据折叠的性质得到∠AFG=∠DFC=30°，CF=AF，EA=EC，∠AEF=∠CEF，再由AD∥BC，得∠CEF=∠AFE，则∠AFE=∠AEF，所以AE=AF，得到四边形AFCE为菱形，有CF=CE，然后根据三角形的内角和定理可计算出∠CEF．
解答：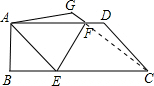
解：连CF，如图，
∵纸片沿EF折叠，使点C与点A重合，点D落在点G处，
∴∠AFG=∠DFC=30°，CF=AF，EA=EC，∠AEF=∠CEF，
而AD∥BC，
∴∠CEF=∠AFE，
∴∠AFE=∠AEF，
∴AE=AF，
∴四边形AFCE为菱形，
∴CF=CE，
∴∠CEF=（180°-30°）÷2=75°．
故答案为75°．
点评：本题考查了折叠的性质：折叠前后两图形全等，即对应角相等，对应线段相等．也考查了和菱形与梯形的性质以及三角形的内角和定理．
分析：连CF，根据折叠的性质得到∠AFG=∠DFC=30°，CF=AF，EA=EC，∠AEF=∠CEF，再由AD∥BC，得∠CEF=∠AFE，则∠AFE=∠AEF，所以AE=AF，得到四边形AFCE为菱形，有CF=CE，然后根据三角形的内角和定理可计算出∠CEF．
解答：
解：连CF，如图，∵纸片沿EF折叠，使点C与点A重合，点D落在点G处，
∴∠AFG=∠DFC=30°，CF=AF，EA=EC，∠AEF=∠CEF，
而AD∥BC，
∴∠CEF=∠AFE，
∴∠AFE=∠AEF，
∴AE=AF，
∴四边形AFCE为菱形，
∴CF=CE，
∴∠CEF=（180°-30°）÷2=75°．
故答案为75°．
点评：本题考查了折叠的性质：折叠前后两图形全等，即对应角相等，对应线段相等．也考查了和菱形与梯形的性质以及三角形的内角和定理．
练习册系列答案
相关题目
得到梯形A2B2C2D2，请你画出梯形A2B2C2D2．
得到梯形A2B2C2D2，请你画出梯形A2B2C2D2．
得到梯形A2B2C2D2 ，请你画出梯形A2B2C2D2．
