Question

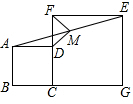如图，已知正方形ABCD和正方形CGEF（CG＞BC），B、C、G 在同一直线上，M 为线段AE的中点，试问：线段MD与线段MF的大小关系，并证明你的结论．

Answer 1

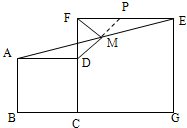答：MF=MD．
证明：延长DM交EF于点P，
∵四边形ABCD和四边形FCGE是正方形，
∴AD∥EF，∠MAD=∠MEP．∠CFE=90°．
∴△DFP是直角三角形．
∵M为AE的中点，
∴AM=EM．
∵在△ADM和△EPM中，
，
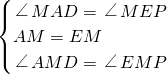∴△ADM≌△EPM（ASA），
∴DM=PM．
∴M是DP的中点．
∴MF=．
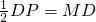分析：延长DM交EF于点P，根据正方形的性质及M 为线段AE的中点可以得出△ADM≌△EPM，由其全等三角形的性质可以得出DP是直角△DFP斜边上的中线，从而得出结论．
点评：本题考查了正方形的性质的运用，相似三角形的判定及性质的运用，直角三角形的性质的运用，解答时正确作辅助线是关键，证明三角形相似是重点．