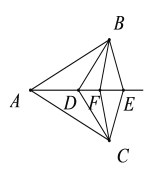Question

【题目】已知在中，，直线经过点（不经过点或点），点关于直线的对称点为，连接．

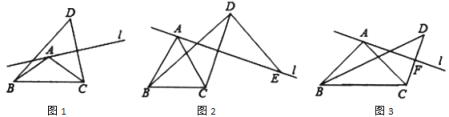
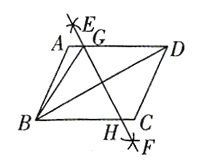
（1）如图1，根据已知可以判断点在以点为圆心，为半径的圆上.请你直接写出的度数（用含的式子表示）.

（2）如图2，当时，过点作的垂线与直线交于点，求证：；

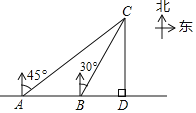
（3）如图3，当时，记直线与的交点为，连接.将直线绕点旋转，当线段的长取得最大值时，直接写出的值.

Answer 1

【答案】（1）；（2）见解析；（3）．

【解析】

（1）由线段垂直平分线的性质可得AD=AC=AB，即可证点B，C，D在以点A为圆心，AB为半径的圆上；由圆周角定理，可求∠BDC的度数；

（2）连接CE，由题意可证△ABC，△DCE是等边三角形，可得AC=BC，∠DCE=60°=∠ACB，CD=CE，根据“SAS”可证△BCD≌△ACE，可得AE=BD；

（3）取AC的中点O，连接OB，OF，BF，由三角形的三边关系可得，当点O，点B，点F三点共线时，BF最长，根据等腰三角形的性质和勾股定理可求，OH=HC，BH=3HC，即可求tan∠FBC的值．

证明：（1）如图1，连接DA，并延长DA交BC于点M，

∵点C关于直线l的对称点为点D，

∴AD=AC，且AB=AC，

∴AD=AB=AC，

∴点B，C，D在以点A为圆心，AB为半径的圆上

∴

故答案为： ．

（2）如图2，连接，

图2

是等边三角形

点关于直线的对称点为点，

，且

是等边三角形，

，且

（3）如图3，取的中点，连接，

图3

在中，

当点，点，点三点共线时，最长，

如图4，过点作，

图4

，且,

点是中点，

．