Question

“文昌阁”是扬州的标志．某天，小芳、小丽来到文昌阁，准备用她们所学的知识测算它的高度．如图，小芳站在A处测得她看塔顶的仰角α为45°，小丽站在B处（A、B与塔的轴心共线）测得她看塔顶的仰角β为30°．她们又测出A、B两点的距离为15米．已知她们的目高（眼睛到地面的距离）均为1.5m，则可计算出塔高约为多少米？（结果精确到1m，参考数据：≈1.4，≈1.7）

Answer 1

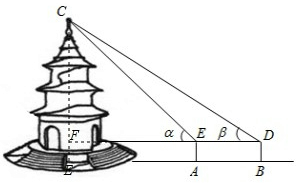解：过点C作CE⊥AB于E，交DE于F，
根据题意得：AE⊥AB，BD⊥AB，DE∥AB，
∴四边形ABDE是矩形，EF=AE=BD=1.5m，CF⊥DE，
∴DE=AB=15m，
设CF=xm，
在Rt△CEF中，EF=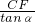==x（m），
在Rt△CDF中，DF=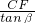==x（m），
∴x-x=15，
解得：x=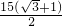≈20.25（m），
∴CE=CF+EF=20.25+1.5=21.75（m）．
答：塔高约为21.75m．
分析：首先过点C作CE⊥AB于E，交DE于F，根据题意可得：AE⊥AB，BD⊥AB，DE∥AB，即可证得四边形ABDE是矩形，EF=AE=BD=1.5m，CF⊥DE，然后设CF=xm，分别在Rt△CEF中与Rt△CDF中，利用正切函数，即可表示出EF与DF的长，继而可得方程：x-x=15，解此方程即可求得答案．
点评：本题考查仰角的定义．此题难度适中，注意要能借助仰角构造直角三角形并解直角三角形是解此题的关键，注意数形结合与方程思想的应用．