题目内容
如图,已知扇形AOB的半径为12,OA⊥OB,C为OB上一点,以OA为直径的半圆O1和以BC为直径的半圆O2相切于点![]() ,求圆中的阴影部分面积.
,求圆中的阴影部分面积.

答案:
解析:
解析:
|
解:连结O1O2,设⊙O2的半径为x,在Rt△O1O2中,O ∵O1O=6,OO2=12-x,O1O2=6+x, ∴(12-x)2+62=(6+x)2,解得x=4, ∴
思路点拨:阴影部分是不规则图形,无法直接求解其面积,可以看作扇形OAB去掉两个半圆的面积,因此,先分别求出⊙O1和⊙O2的半径. 评注:(1)对于一个不规则图形,无法直接求出其面积时,常常将它分解成几个规则图形的和或差. (2)在本题中,求出⊙O2的半径是关键,特别要学会利用相切的重要性质,列出方程求解. |

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目

 19、如图,已知扇形AOB的半径为12,OA⊥OB,C为OA上一点,以AC为直径的半圆O1,和以OB为直径的半圆O2相切,则半圆O1的半径为
19、如图,已知扇形AOB的半径为12,OA⊥OB,C为OA上一点,以AC为直径的半圆O1,和以OB为直径的半圆O2相切,则半圆O1的半径为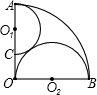 如图,已知扇形AOB的半径为12,OA⊥OB,C为OA上一点,以AC为直径的半圆O1和以OB为直径的半圆O2相切,则半圆O1的半径为( )
如图,已知扇形AOB的半径为12,OA⊥OB,C为OA上一点,以AC为直径的半圆O1和以OB为直径的半圆O2相切,则半圆O1的半径为( ) 如图,已知扇形AOB,OA⊥OB,C为OB上一点,以OA为直线的半圆O1与以BC为直径的半圆O2相切于点D.
如图,已知扇形AOB,OA⊥OB,C为OB上一点,以OA为直线的半圆O1与以BC为直径的半圆O2相切于点D. (2012•龙岩模拟)如图,已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥.则围成的圆锥的表面积为( )
(2012•龙岩模拟)如图,已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥.则围成的圆锥的表面积为( ) 如图,已知扇形AOB的半径为12,OA⊥OB,C为OB上一点,以OA为直径的半圆O1与以BC为直径的半圆O2相切于点D,求图中阴影部分的面积.
如图,已知扇形AOB的半径为12,OA⊥OB,C为OB上一点,以OA为直径的半圆O1与以BC为直径的半圆O2相切于点D,求图中阴影部分的面积.