Question

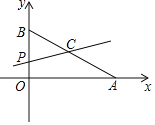
【题目】如图，已知直线l与⊙O相离，OA⊥l于点A，OA＝10，OA与⊙O相交于点P，AB与⊙O切于点B，BP的延长线交直线l于点C．

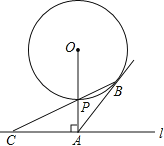
（1）试判断线段AB与AC的数量关系，并说明理由；

（2）若PC＝4，求⊙O的半径和线段PB的长．

Answer 1

【答案】（1）AB＝AC，理由见解析；（2）.

【解析】

（1）连接，根据切线的性质和垂直得出，推出，求出，根据等腰三角形的判定推出即可

（2）延长AP交⊙O于E，连接BDE，设圆半径为r，则OP=OB=r，PA=10﹣r，根据AB=AC推出，求出r，证△EPB∽△CPA，得出关于BP的比例式，代入求出即可．

解：（1）AB＝AC，理由如下：

如图1，连接OB．

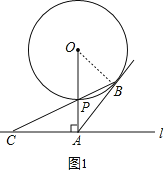
∵AB切⊙O于B，OA⊥l，

∴∠OBA＝∠OAC＝90°，

∴∠OBP+∠ABP＝90°，∠ACP+∠APC＝90°，

∵OP＝OB，

∴∠OBP＝∠OPB，

∵∠OPB＝∠APC，

∴∠ACP＝∠ABC，

∴AB＝AC；

（2）如图2，延长AP交⊙O于E，连接BE，

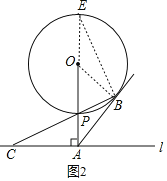
设圆半径为r，则OP＝OB＝r，PA＝10﹣r，

则AB2＝OA2﹣OB2＝102﹣r2，

∵AC2+PA2＝PC2，

∴，

解得：r＝6，

∴AB＝AC＝8，PA＝OA﹣OP＝4，

∵PE是⊙O的直径，

∴∠PBE＝90°＝∠PAC，

又∵∠EPB＝∠CPA，

∴△EPB∽△CPA，

∴ ，

∴ ，

∴ ．