题目内容
方程(x-5)(x+2)=0化为一般形式是________,其中a=________,b=________,c=________,b2-4ac=________,方程的根为________.
x2-3x-10=0 1 -3 -10 49 x1=5,x2=-2
分析:方程整理为一般形式,找出a,b,c的值,计算出根的判别式的值大于0,代入求根公式即可求出解.
解答:方程(x-5)(x+2)=0,
整理得:x2-3x-10=0,
其中a=1,b=-3,c=-10,
∵b2-4ac=9+40=49,
∴x=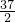 ,
,
则方程的解为x1=5,x2=-2.
故答案为:x2-3x-10=0;1,-3,-10,49;x1=5,x2=-2
点评:此题考查了一元二次方程的一般形式,以及根的判别式,弄清题意是解本题的关键.
分析:方程整理为一般形式,找出a,b,c的值,计算出根的判别式的值大于0,代入求根公式即可求出解.
解答:方程(x-5)(x+2)=0,
整理得:x2-3x-10=0,
其中a=1,b=-3,c=-10,
∵b2-4ac=9+40=49,
∴x=
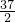 ,
,则方程的解为x1=5,x2=-2.
故答案为:x2-3x-10=0;1,-3,-10,49;x1=5,x2=-2
点评:此题考查了一元二次方程的一般形式,以及根的判别式,弄清题意是解本题的关键.

练习册系列答案
相关题目
下列方程中,以x表示y的是( )
| A、x+y=8 | ||
B、x=
| ||
| C、2y=5x+7 | ||
| D、y=2x-1 |
关于x的分式方程
=
无解,则m的值为( )
| 2x |
| x+1 |
| m |
| x+1 |
| A、-2 | B、-1 | C、0 | D、2 |
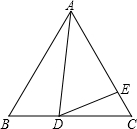 已知:等边△ABC中,AB、cosB是关于x的方程x2-4mx-
已知:等边△ABC中,AB、cosB是关于x的方程x2-4mx-