题目内容
 如图,点C是线段AB延长线上的一点,M、N分别是线段AB、AC的中点.若MN=4cm,且AB=
如图,点C是线段AB延长线上的一点,M、N分别是线段AB、AC的中点.若MN=4cm,且AB=| 3 | 4 |
32
32
cm.分析:根据题意即可推出AN-AM=MN=4cm,由AB=
AC,推出2AM=
×2AN,然后把AM和AN看做是未知数,解二元一次方程即可推出AN的程度,继而求出AC的长度.
| 3 |
| 4 |
| 3 |
| 4 |
解答:解:∵M、N分别是线段AB、AC的中点,
∴AC=2AN,AB=2AM,
∵MN=4cm,
∴AN-AM=MN=4cm,
∵AB=
AC,
∴2AM=
×2AN,
∴AM=
AN,
解二元一次方程组:
得:
,
∴AC=2AN=32cm.
故答案为32.
∴AC=2AN,AB=2AM,
∵MN=4cm,
∴AN-AM=MN=4cm,
∵AB=
| 3 |
| 4 |
∴2AM=
| 3 |
| 4 |
∴AM=
| 3 |
| 4 |
解二元一次方程组:
|
|
∴AC=2AN=32cm.
故答案为32.
点评:本题主要考查解二元一次方程组,两点之间的距离,线段中点的性质,关键在于运用数形结合的思想列出二元一次方程组.

练习册系列答案
相关题目
如图,点C是线段AB的中点,点D是线段BC的中点,下面等式不正确的是( )
| A、CD=AD-BC | ||
| B、CD=AC-DB | ||
C、CD=
| ||
D、CD=
|
 10、如图,点D是线段AB与线段BC的垂直平分线的交点,∠B=40°,则∠ADC等于( )
10、如图,点D是线段AB与线段BC的垂直平分线的交点,∠B=40°,则∠ADC等于( )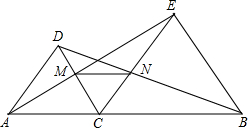 AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.
AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N. 如图,点C是线段AB的中点,点D是线段CB上任意一点,则下列表示线段关系的式子不正确的是( )
如图,点C是线段AB的中点,点D是线段CB上任意一点,则下列表示线段关系的式子不正确的是( ) 如图,点C是线段AB的中点,点D是线段BC的中点,则下列结论中错误的是( )
如图,点C是线段AB的中点,点D是线段BC的中点,则下列结论中错误的是( )