题目内容
在梯形ABCD中,已知AD∥BC,∠C=60°,AB⊥BC,CD=4cm,AD=3cm,则梯形ABCD的面积为
- A.

- B.
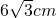
- C.

- D.
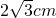
C
分析:过点D作DE⊥BC,垂足为E,则四边形ADEB是矩形,所以AD=BE=3cm,在直角三角形DEC中利用60°角的锐角三角函数值可以求出DE和CE,再根据梯形的面积公式求解即可.
解答:过D点作BC的垂线交BC于E,
∵AD∥BC,AB⊥BC,
∴四边形ADEB是矩形,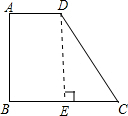
∴AD=BE=3cm,
∵∠C=60°,∠DEC=90°,CD=4cm,
∴∠CDE=30°,
∴CE= CD=2cm,
CD=2cm,
∴BC=BE+CE=5cm,
∵sin60=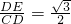 ,
,
∴DE=2 ,
,
∴∴S梯形ABCD= (AD+BC)•DE=8
(AD+BC)•DE=8 cm2,
cm2,
答:梯形ABCD的面积为8 cm2.
cm2.
故选C.
点评:本题是对直角梯形的考查和锐角三角函数的运用,作出辅助线,构造出梯形的高,并求解是解题的关键.
分析:过点D作DE⊥BC,垂足为E,则四边形ADEB是矩形,所以AD=BE=3cm,在直角三角形DEC中利用60°角的锐角三角函数值可以求出DE和CE,再根据梯形的面积公式求解即可.
解答:过D点作BC的垂线交BC于E,
∵AD∥BC,AB⊥BC,
∴四边形ADEB是矩形,

∴AD=BE=3cm,
∵∠C=60°,∠DEC=90°,CD=4cm,
∴∠CDE=30°,
∴CE=
 CD=2cm,
CD=2cm,∴BC=BE+CE=5cm,
∵sin60=
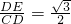 ,
,∴DE=2
 ,
,∴∴S梯形ABCD=
 (AD+BC)•DE=8
(AD+BC)•DE=8 cm2,
cm2,答:梯形ABCD的面积为8
 cm2.
cm2.故选C.
点评:本题是对直角梯形的考查和锐角三角函数的运用,作出辅助线,构造出梯形的高,并求解是解题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 22、如图,在梯形ABCD中,已知AB∥CD,AD=BC,AC、BD相交于点O.求证:OD=OC.
22、如图,在梯形ABCD中,已知AB∥CD,AD=BC,AC、BD相交于点O.求证:OD=OC. (2012•苏州)如图,在梯形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE、AC.
(2012•苏州)如图,在梯形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE、AC. 如图,在梯形ABCD中,已知AD∥BC,∠B=90°,AB=7,AD=9,BC=12,在线段BC上任取一点E,连接DE,作EF⊥DE,交直线AB于点F.
如图,在梯形ABCD中,已知AD∥BC,∠B=90°,AB=7,AD=9,BC=12,在线段BC上任取一点E,连接DE,作EF⊥DE,交直线AB于点F. 如图所示,在梯形ABCD中,已知AD∥BC,AB=DC,∠ACB=40°,∠ACD=30°.
如图所示,在梯形ABCD中,已知AD∥BC,AB=DC,∠ACB=40°,∠ACD=30°. 如图,在梯形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE、AC.
如图,在梯形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE、AC.