题目内容
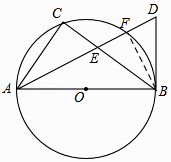
【题目】如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E. 
(1)求证:BD=BE;
(2)若DE=2,BD= ![]() ,求CE的长.
,求CE的长.
【答案】
(1)解:设∠BAD=α,
∵AD平分∠BAC
∴∠CAD=∠BAD=α,
∵AB是⊙O的直径,∴∠ACB=90°,
∴∠ABC=90°﹣2α,
∵BD是⊙O的切线,
∴BD⊥AB,
∴∠DBE=2α,
∠BED=∠BAD+∠ABC=90°﹣α,
∴∠D=180°﹣∠DBE﹣∠BED=90°﹣α,
∴∠D=∠BED,
∴BD=BE
(2)解:设AD交⊙O于点F,CE=x,则AC=2x,连接BF,
∵AB是⊙O的直径,
∴∠AFB=90°,
∵BD=BE,DE=2,
∴FE=FD=1,
∵BD= ![]() ,
,
∴tanα= ![]() ,
,
∴AB= ![]() =2
=2 ![]()
在Rt△ABC中,
由勾股定理可知:(2x)2+(x+ ![]() )2=(2
)2=(2 ![]() )2,
)2,
∴解得:x=﹣ ![]() 或x=
或x= ![]() ,
,
∴CE= ![]() ;
;
【解析】(1))设∠BAD=α,由于AD平分∠BAC,所以∠CAD=∠BAD=α,进而求出∠D=∠BED=90°﹣α,从而可知BD=BE;(2)设CE=x,由于AB是⊙O的直径,∠AFB=90°,又因为BD=BE,DE=2,FE=FD=1,由于BD= ![]() ,所以tanα=
,所以tanα= ![]() ,从而可求出AB=
,从而可求出AB= ![]() =2
=2 ![]() ,利用勾股定理列出方程即可求出x的值.
,利用勾股定理列出方程即可求出x的值.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目





