题目内容
如下图，点P为∠ABC角平分线上的一点，D点和E点分别在AB和BC上，且PD=PE，试探究∠BDP与∠BEP的数量关系，并给予证明．
解：∠BDP+∠BEP=180°．理由：过P作PM⊥AB于点M，PN⊥BC于N点，
由角平分线性质，得PM=PN
在Rt△DPM和Rt△EPN中
∴Rt△DPM≌Rt△EPN（HL）
∠ADP=∠BEP，
又∠BDP+∠ADP=180°，
∴∠BDP+∠BEP=180°．
分析：根据角平分线性质，过P作PM⊥AB于点M，PN⊥BC于N点，则PM=PN，已知PD=PE，可证Rt△DPM≌Rt△EPN，再利用对应角相等及平角的性质证明∠BDP+∠BEP=180°．
点评：本题考查了角平分线性质的运用和三角形全等的性质及判定，转化的思想的应用．正确作出辅助线是解决问题的关键．
练习册系列答案
相关题目
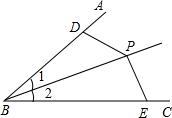如下图，点P为∠ABC角平分线上的一点，D点和E点分别在AB和BC上，且PD=PE，试探究∠BDP与∠BEP的数量关系，并给予证明．
＝
，那么称直线l为该图形的黄金分割线．
