题目内容
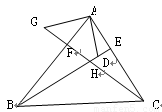
如图BE、CF分别是△ABC的高,M为BC中点,BC=10,  ,求△EFM的面积。
,求△EFM的面积。
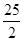
解析考点:直角三角形斜边上的中线;三角形的面积;勾股定理;等腰直角三角形.
分析:过M作MD⊥EF于D,根据直角三角形斜边上的中线定理求出ME和MF的长,再求出DE长根据勾股定理即可求出高MD,利用面积公式即可求出答案.
解答: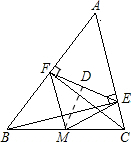
解:过M作MD⊥EF于D,
∵BE、CF分别是△ABC的高,
∴∠BFC=∠BEC=90°,
∵M为BC的中点,BC=10,
∴ME=MF=5,
∵EF=5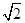 ,
,
∴DE=DF=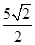 ,
,
在△MDE中由勾股定理得:MD=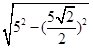 =
=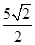 ,
,
∴△EFM的面积是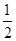 EF?DM=
EF?DM=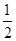 ×5
×5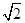 ×
×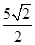 =
=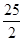 .
.
答:△EFM的面积是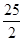 .
.
点评:本题主要考查了等腰三角形的性质,直角三角形斜边上的中线,勾股定理,三角形的面积等知识点,解此题的关键是求出边EF上的高.难点是作辅助线DM.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
 23、已知如图BE、CF分别是∠ABD、∠ACD的平分线.
23、已知如图BE、CF分别是∠ABD、∠ACD的平分线.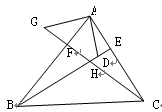
 ,求△EFM的面积。
,求△EFM的面积。
 ,求△EFM的面积。
,求△EFM的面积。