Question

【题目】如图所示，有一张矩形纸片ABCD，E、F分别是BC、AD上的点（不与顶点重合）．如果直线EF将矩形分成面积相等的两部分，那么

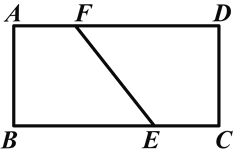
（1）得到的两个四边形是否相似？若相似，请求出相似比；若不相似，请说明理由；

（2）这样的直线可以作多少条？

Answer 1

【答案】见解析

【解析】（1）相似．理由如下：

因为EF将矩形ABCD分成面积相等的两部分，所以可设AB＝a，AD＝b，BE＝x．

于是有，

所以x＋AF＝b－x＋b－AF，即AF＝b－x．

又EC＝b－x，所以AF＝EC．

在矩形ABCD中，AB＝CD，AD＝BC，AD∥BC，

所以DF＝BE，∠AFE＝∠FEC，∠DFE＝∠BEF，∠A＝∠B＝∠C＝∠D＝90°．

所以在四边形ABEF与四边形CDFE中，有

∠A＝∠C＝90°，∠B＝∠D＝90°，∠AFE＝∠FEC，∠BEF＝∠DFE，

，

所以四边形ABEF与四边形CDFE相似，相似比为1．

（2）这样的直线有无数条，只要过矩形对角线的交点且满足条件即可．