题目内容
7. 在横线上填上适当内容,在括号内填写理由:
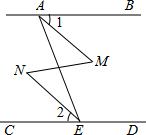
在横线上填上适当内容,在括号内填写理由:已知:如图,∠BAE+∠AED=180°,∠1=∠2,求证:∠M=∠N.
证明∵∠BAE+∠AED=180°(已知)
∴AB∥CD(同旁内角互补、两直线平行)
∴∠BAE=∠AEC
又∵∠1=∠2(已知)
∴∠BAE-∠1=∠AEC-∠2 (等式的性质)
即∠MAE=∠AEN
∴AM∥EN
∴∠M=∠N (两直线平行,内错角相等).
分析 根据平行线的判定定理和性质定理即可直接解答.
解答 证明∵∠BAE+∠AED=180°(已知)
∴AB∥CD( 同旁内角互补、两直线平行)
∴∠BAE=∠AEC
又∵∠1=∠2(已知)
∴∠BAE-∠1=∠AEC-∠2 ( 等式的性质)
即∠MAE=∠AEN
∴AM∥EN
∴∠M=∠N ( 两直线平行,内错角相等).
故答案是:同旁内角互补、两直线平行;等式的性质; 两直线平行,内错角相等.
点评 本题考查了平行线的性质定理和判定定理,理解定理是关键.

练习册系列答案
相关题目
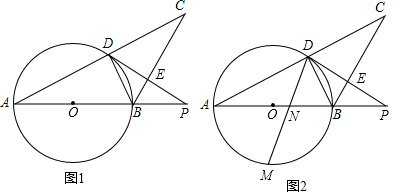
 如图,点O是矩形纸片ABCD的对称中心,E是BC上一点,将纸片沿AE折叠后,点B恰好与点O重合.若BE=3,则折痕AE的长为6.
如图,点O是矩形纸片ABCD的对称中心,E是BC上一点,将纸片沿AE折叠后,点B恰好与点O重合.若BE=3,则折痕AE的长为6.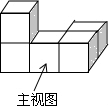 下列是由5个完全相同的正方体组成的立体图形,它的俯视图是( )
下列是由5个完全相同的正方体组成的立体图形,它的俯视图是( )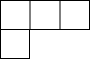
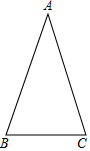 已知等腰△ABC的顶角∠A=36°(如图).
已知等腰△ABC的顶角∠A=36°(如图).