题目内容
 如图是一个“黄金三角形”:AB=AC,∠A=36°.若CD平分∠ACB,交AB于点D.
如图是一个“黄金三角形”:AB=AC,∠A=36°.若CD平分∠ACB,交AB于点D.(1)求∠BCD的度数;
(2)除△ABC外,你还能找到几个等腰三角形,并分别证明之.
分析:(1)根据等腰三角形性质和三角形内角和定理求出∠ACB,根据角平分线定义求出即可.
(2)根据三角形外角性质求出∠BDC=∠B=72°,求出∠A=∠ACD=36°,根据等腰三角形的判定推出即可.
(2)根据三角形外角性质求出∠BDC=∠B=72°,求出∠A=∠ACD=36°,根据等腰三角形的判定推出即可.
解答:解:(1)∵在△ABC中,AB=AC,∠A=36°,
∴∠ABC=∠ACB=(180°-∠A)÷2=72°,
∵△ABC的角平分线BD与CE相交于点O,
∴∠BCD=∠ACD=
∠ACB=36°.
(2)等腰三角形有△ACD和△BDC,
证明:∵∠A=∠ACD=36°,
∴△ACD是等腰三角形,
∵∠A=∠ACD=36°,
∴∠BDC=∠A+∠ACD=72°,
∵∠B=72°,
∴∠B=∠BDC,
∴△BDC是等腰三角形.
∴∠ABC=∠ACB=(180°-∠A)÷2=72°,
∵△ABC的角平分线BD与CE相交于点O,
∴∠BCD=∠ACD=
| 1 |
| 2 |
(2)等腰三角形有△ACD和△BDC,
证明:∵∠A=∠ACD=36°,
∴△ACD是等腰三角形,
∵∠A=∠ACD=36°,
∴∠BDC=∠A+∠ACD=72°,
∵∠B=72°,
∴∠B=∠BDC,
∴△BDC是等腰三角形.
点评:此题考查了学生读题做题的能力以及等腰三角形的性质与判定.此题难度适中,正确理解“黄金三角形”的定义是解题的关键

练习册系列答案
相关题目
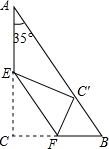 如图是一个直角三角形的纸片,将直角沿EF折叠,使C点落在AB边上,并且使∠EC′A=∠A,那么∠C′FE的度数是( )
如图是一个直角三角形的纸片,将直角沿EF折叠,使C点落在AB边上,并且使∠EC′A=∠A,那么∠C′FE的度数是( )| A、50° | B、45° | C、55° | D、70°第7题图 |

 如图是一个直角三角形纸片,∠C=90°,两直角边长分别是3cm,4cm.现要给它再拼接一个完全一样直角三角形纸片,两纸片不重叠且无缝隙,使得拼成的图形形状是等腰三角形,则拼成的等腰三角形的周长为
如图是一个直角三角形纸片,∠C=90°,两直角边长分别是3cm,4cm.现要给它再拼接一个完全一样直角三角形纸片,两纸片不重叠且无缝隙,使得拼成的图形形状是等腰三角形,则拼成的等腰三角形的周长为 如图是一个“黄金三角形”:AB=AC,∠A=36°.若CD平分∠ACB,交AB于点D.
如图是一个“黄金三角形”:AB=AC,∠A=36°.若CD平分∠ACB,交AB于点D.