Question

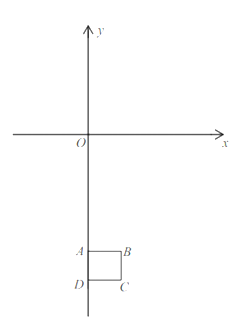
【题目】已知，正方形，，抛物线为常数)，顶点为．

（1）拋物线经过定点坐标是___ __，顶点的坐标(用的代数式表示)是____ _．

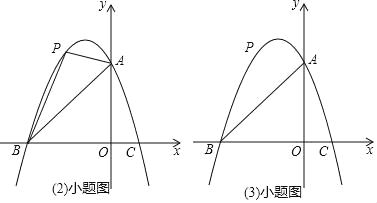
（2）若抛物线(为常数)与正方形的边有交点，则的取值范围是___ _．

（3）若时，求的值．

Answer 1

【答案】（1），；（2）；（3）或

【解析】

（1）判断函数图像过定点，可以分析代入x的值使得含m的同类项合并后系数为0；

（2）由（1）中的m表示的顶点坐标，可以得到m变化时，抛物线顶点在上运动，分析该函数图像和正方形ABCD的顶点位置关系即可解答；

（3）需要分类讨论，由已知点M在过点B且与AB夹角为45°的直线与抛物线在的交点上，可解决问题.

解:

当时，

抛物线经过定点坐标是．

抛物线的解析式为，

顶点的对称轴为直线

当时，

故答案为: ；

设，

则，带入=

整理得

即抛物线的顶点在抛物线上运动．其对称轴为直线，

当抛物线顶点直线右侧时即时，

抛物线与正方形无交点．

当时，观察抛物线的顶点所在抛物线恰好过点

，此时

当抛物线过点时

得

抛物线为常数)与正方形的边有交点时

的范围为:

由抛物线顶点在抛物线上运动

当点在线段上方时，

过点且使的直线解析式为

联立方程

得交点横坐标的(舍去)

当点在线段下方时

过点且使的直线解析式为

联立方程

得交点横坐标的(舍去)

的值为或