题目内容
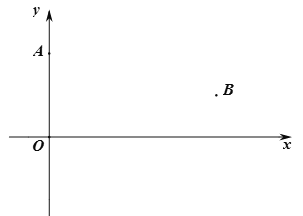
【题目】如图，点
的坐标为
，点
的坐标为
，点
是
轴上一点，且
的值最小，
（1）确定点的位置，并求点的坐标；
（2）求的最小值．
【答案】（1）作图见解析，P
；（2）最小值为
【解析】
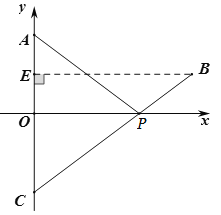
（1）如图，作点A关于x轴的对称点C，连接BC交x轴于点P，则点
就是所要求作的点，由轴对称的性质易得点C坐标，然后利用待定系数法求出直线BC的解析式，再求出其与x轴的交点即可；
（2）过点
作BE⊥y轴，垂足为点
，则点E坐标易求，于是CE、BE可得，然后在
中根据勾股定理即可求出BC，即为
的最小值．
解:（1）如图，作点A关于x轴的对称点C，连接BC交x轴于点P，则点就是所要求作的点，
点
与点
关于
轴对称，
点的坐标为
．
设直线
的表达式为：
，将点的坐标
代入，得：
，解得：
，
直线的表达式为：
．
令
，解得
，∴点的坐标为；
(2)过点作BE⊥y轴，垂足为点，点的坐标是
，
∵B（8，2），，
．
在中，由勾股定理得：
．
由于
．
所以的最小值为．
练习册系列答案
相关题目
