Question

【题目】如图，半径为的中，弦，所对的圆心角分别是，，若，，则弦的长等于（ ）

A. B. C. D.

Answer 1

【答案】A

【解析】

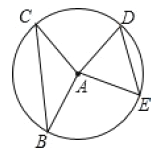
作AH⊥BC于H，作直径CF，连结BF，先利用等角的补角相等得到∠DAE=∠BAF，然后再根据同圆中，相等的圆心角所对的弦相等得到DE=BF=6，由AH⊥BC，根据垂径定理得CH=BH，易得AH为△CBF的中位线，然后根据三角形中位线性质得到AH=BF=3，从而求解．

解：作AH⊥BC于H，作直径CF，连结BF，如图，

∵∠BAC+∠EAD=180°，而∠BAC+∠BAF=180°，

∴∠DAE=∠BAF，∴弧DE＝弧BF，∴DE=BF=6，

∵AH⊥BC，∴CH=BH，

∵CA=AF，∴AH为△CBF的中位线，∴AH=BF=3．

∴，

∴BC＝2BH＝8．

故选A．

“点睛”本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了垂径定理和三角形中位线性质．