题目内容
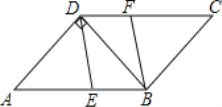
【题目】如图，在平行四边形
中，
，
，且
于点
，点
分别是边
上的动点，且
.
①求证：四边形
是平行四边形；
②当
为何值时，四边形是矩形？
【答案】①证明见解析；②
.
【解析】
（1）根据平行四边形的对边平行且相等可得AB∥CD，AB=CD，再求出BE=DF，然后根据一组对边平行且相等的四边形是平行四边形证明；
（2）过D作DE⊥AB于E，根据直角三角形两锐角互余求出∠ADE=30°，再根据直角三角形30°角所对的直角边等于斜边的一半可得AE=
AD．
(1)证明：
四边形ABCD是平行四边形
四边形DEBF为平行四边形.
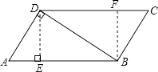
(2)当
时，四边形DEBF为矩形. 理由是：
过点D作
于点 E
在
中，
AD⊥DB，∠ADB=90°
在
中，
当
时，
，
即平行四边形DEBF是矩形.
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
