题目内容
7.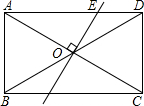 如图,矩形ABCD中,AB=3,BC=4,对角线AC和BD相交于点O,过O作OE⊥AC交AD于E,则AE=$\frac{25}{8}$.
如图,矩形ABCD中,AB=3,BC=4,对角线AC和BD相交于点O,过O作OE⊥AC交AD于E,则AE=$\frac{25}{8}$.
分析 连接CE,根据矩形性质得出AD=BC=5,∠ADC=90°,CD=AB=3,OA=OC,根据线段垂直平分线性质得出AE=CE,在△EDC中,根据勾股定理得出方程,求出即可.
解答 解: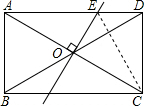 连接EC,
连接EC,
∵四边形ABCD是矩形,AB=3,BC=4,
∴AD=BC=4,∠ADC=90°,CD=AB=3,OA=OC,
∵OE⊥AC,
∴OE是线段AC的垂直平分线,
∴AE=CE,
设AE=CE=a,则DE=4-a,
在Rt△EDC中,由勾股定理得:CE2=DE2+CD2,
即a2=(4-a)2+32,
a=$\frac{25}{8}$,
即AE=$\frac{25}{8}$,
故答案为:$\frac{25}{8}$.
点评 本题考查了矩形性质,勾股定理,线段垂直平分线性质等知识点,用了方程思想,题目比较典型,是一道比较好的题目.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴的对称图形△A1B1C1,再画出△A1B1C1向右平移1个单位的△A2B2C2.
如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴的对称图形△A1B1C1,再画出△A1B1C1向右平移1个单位的△A2B2C2. 已知:如图,在平面直角坐标系中,正方形ABCD的边长为8.求出AC和BD的长度,并直接写出它的四个顶点A、B、C、D的坐标.
已知:如图,在平面直角坐标系中,正方形ABCD的边长为8.求出AC和BD的长度,并直接写出它的四个顶点A、B、C、D的坐标.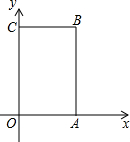 如图,在矩形ABCD中,O为坐标原点,A,C两点坐标分别为(3,0)和(0,5).
如图,在矩形ABCD中,O为坐标原点,A,C两点坐标分别为(3,0)和(0,5).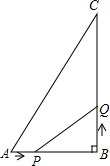 如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,设移动时间为t(s).
如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,设移动时间为t(s).