题目内容
方程m|x|-x-m=0(m>0且m≠1)有两个解,则实数m的取值范围是( )
| A.m>1 | B.0<m<1 |
| C.0<m<1或m<1 | D.这样的m不存在 |
由方程m|x|-x-m=0(m>0且m≠1)有两个解,可得知有一个正跟与一个负根,
当x>0时,解方程得:x=
(m>0且m≠1),则m>1;
当x<0时,解方程得;x=
<0,则m>-1,综上所述,
∴m>1.
故选A.
当x>0时,解方程得:x=
| m |
| m-1 |
当x<0时,解方程得;x=
| -m |
| m+1 |
∴m>1.
故选A.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
下列方程中,以x表示y的是( )
| A、x+y=8 | ||
B、x=
| ||
| C、2y=5x+7 | ||
| D、y=2x-1 |
关于x的分式方程
=
无解,则m的值为( )
| 2x |
| x+1 |
| m |
| x+1 |
| A、-2 | B、-1 | C、0 | D、2 |
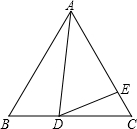 已知:等边△ABC中,AB、cosB是关于x的方程x2-4mx-
已知:等边△ABC中,AB、cosB是关于x的方程x2-4mx-