题目内容
已知△ABC中,AB=c,AC=b,BC=a. BC边的高为ha,AC边的高为hb.且有a≤ha,b≤hb,求△ABC的三个内角的度数.
解:设三角形面积为S,
∵ •a•ha=
•a•ha= •b•hb=S,
•b•hb=S,
∴ha=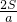 ,hb=
,hb= ,
,
而a≤ha,b≤hb,
∴a2≤2S,b2≤2S,
∵a,b,2S均大于0,
∴a2•b2≤4S,
∴ab≤2S,
而2S=ab•sinC,即ab≤ab•sinC,
∴sinC≥1,而sinC≤1,
∴sinC=1,
∴∠C=90°,
∴ha=b,hb=a,
∴a≤b,b≤a,
∴a=b,
∴△ABC为等腰直角三角形,
∴△ABC的三个内角的度数为:∠C=90°,∠A=∠B=45°.
分析:设三角形面积为S,根据三角形的面积公式得到 •a•ha=
•a•ha= •b•hb=S,即ha=
•b•hb=S,即ha=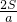 ,hb=
,hb= ,由a≤ha,b≤hb,得到a2≤2S,b2≤2S,得到a2•b2≤4S,所以有ab≤2S,而2S=ab•sinC,即ab≤ab•sinC,即可得到sinC=1,∠C=90°,根据直角三角形的性质得到ha=b,hb=a,则a≤b,b≤a,即可判断△ABC为等腰直角三角形,从而易得到△ABC的三个内角的度数.
,由a≤ha,b≤hb,得到a2≤2S,b2≤2S,得到a2•b2≤4S,所以有ab≤2S,而2S=ab•sinC,即ab≤ab•sinC,即可得到sinC=1,∠C=90°,根据直角三角形的性质得到ha=b,hb=a,则a≤b,b≤a,即可判断△ABC为等腰直角三角形,从而易得到△ABC的三个内角的度数.
点评:本题考查了三角形的面积公式:三角形的面积等于底乘以底边上的高的一半.也考查了直角三角形的面积公式,90度的正弦值以及等腰直角三角形的性质.
∵
 •a•ha=
•a•ha= •b•hb=S,
•b•hb=S,∴ha=
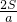 ,hb=
,hb= ,
,而a≤ha,b≤hb,
∴a2≤2S,b2≤2S,
∵a,b,2S均大于0,
∴a2•b2≤4S,
∴ab≤2S,
而2S=ab•sinC,即ab≤ab•sinC,
∴sinC≥1,而sinC≤1,
∴sinC=1,
∴∠C=90°,
∴ha=b,hb=a,
∴a≤b,b≤a,
∴a=b,
∴△ABC为等腰直角三角形,
∴△ABC的三个内角的度数为:∠C=90°,∠A=∠B=45°.
分析:设三角形面积为S,根据三角形的面积公式得到
 •a•ha=
•a•ha= •b•hb=S,即ha=
•b•hb=S,即ha=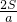 ,hb=
,hb= ,由a≤ha,b≤hb,得到a2≤2S,b2≤2S,得到a2•b2≤4S,所以有ab≤2S,而2S=ab•sinC,即ab≤ab•sinC,即可得到sinC=1,∠C=90°,根据直角三角形的性质得到ha=b,hb=a,则a≤b,b≤a,即可判断△ABC为等腰直角三角形,从而易得到△ABC的三个内角的度数.
,由a≤ha,b≤hb,得到a2≤2S,b2≤2S,得到a2•b2≤4S,所以有ab≤2S,而2S=ab•sinC,即ab≤ab•sinC,即可得到sinC=1,∠C=90°,根据直角三角形的性质得到ha=b,hb=a,则a≤b,b≤a,即可判断△ABC为等腰直角三角形,从而易得到△ABC的三个内角的度数.点评:本题考查了三角形的面积公式:三角形的面积等于底乘以底边上的高的一半.也考查了直角三角形的面积公式,90度的正弦值以及等腰直角三角形的性质.

练习册系列答案
相关题目
 如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程证明△ABD≌△ACD的理由.
如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程证明△ABD≌△ACD的理由. 已知△ABC中,AB=AC,AD为BC边上的中线,BE为AC边上的高,
已知△ABC中,AB=AC,AD为BC边上的中线,BE为AC边上的高, 如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程,说明△ABD≌△ACD的理由.
如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程,说明△ABD≌△ACD的理由.
 如图:已知△ABC中,AB=17cm,BC=30cm,BC边上的中线AD=8cm.求证:△ABC是等腰三角形.
如图:已知△ABC中,AB=17cm,BC=30cm,BC边上的中线AD=8cm.求证:△ABC是等腰三角形.