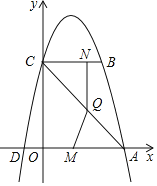Question

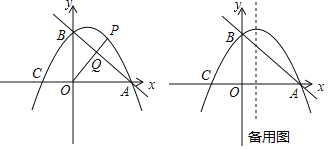
【题目】如图，抛物线的顶点为，交轴于点，（点在点的右侧），点在第一象限，且在抛物线部分上，交轴于点．

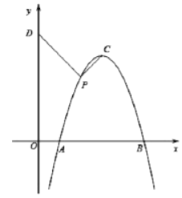
（1）求该抛物线的表达式．

（2）若，求的长．

Answer 1

【答案】（1）；（2）5

【解析】

（1）已知抛物线顶点坐标，可得，，解出a和c，即可求出抛物线解析式．

（2）作PH⊥OD，交OD于点H，CF⊥PH，交PH于点F，设P（a，），根据，列出关于a的关系式，求出a，分别求出DH和OH ，OD=OH+HD即可求解．

（1）由题意，得，

由（1），得（3），

把（3）代入（2），得

∴抛物线的表达式

故答案为：

（2）作PH⊥OD，交OD于点H，CF⊥PH，交PH于点F，

设P（a，）

由题意，得，

化简，得，

解得a=2，或，

∵在抛物线部分上，

∴舍去

DH=2PF=2（3-a）=2，OH==3，

∴OD=OH+HD=3+2=5．