Question

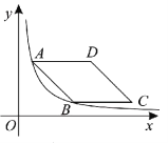
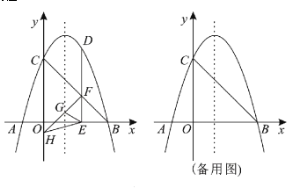
【题目】如图，在平面直角坐标系中，抛物线与轴交于，两点，与轴交于点．

（1）直接写出抛物线的解析式为：；

（2）点为第一象限内抛物线上的一动点，作轴于点，交于点，过点作的垂线与抛物线的对称轴和轴分别交于点，，设点的横坐标为．

①求的最大值；

②连接，若，求的值．

Answer 1

【答案】（1）；（2）①；②，

【解析】

（1）将点，代入抛物线，求出b、c的值，继而求出抛物线解析式；

（2）①先求出点C的坐标，由待定系数法求出直线BC的解析式，作轴于点，可得： ，由线段的和差可得：，代入数据得到二次函数，由二次函数的性质可知当，有最大值；

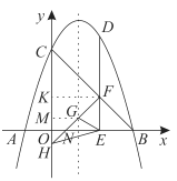
②作轴于点，记直线与轴交于点，易知，由等角对等边可知：EN＝EF，OH＝ON，由抛物线的性质可得MG＝1，继而可得HG＝，根据相似三角形的判定及其性质可得，，代入数据可得，在中，由勾股定理可得，可得一元二次方程，继而解方程求解．

（1）将点，代入抛物线得：

解得：

故抛物线的解析式为：；

（2）①当时，

点，又点，

的解析式为：，

，

，

作轴于点，又，

，

，

，

化简得：，

由题意有，且，，

当时，取最大值，

的最大值为

②作轴于点，记直线与轴交于点，

轴，轴，，

，

，

，

，的对称轴为，

，，

，又∠EHF＝∠GHE，

，

，

在中，，

，

解得：或