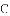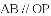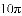��Ŀ����
���Ķ�����һ�β��ϣ�����ɺ�������⣺
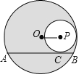
���ϣ���������y=ax2��a��0���ĶԳ�����һ�㣨0����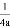 �����Գ���Ĵ���l����������������һ��P����F��0��
�����Գ���Ĵ���l����������������һ��P����F��0��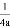 ���ľ�����P��l�ľ���һ����ȣ����ǽ���F��ֱ��l�ֱ�����������ߵĽ�����ߣ���y=x2�Ľ���Ϊ��0��
���ľ�����P��l�ľ���һ����ȣ����ǽ���F��ֱ��l�ֱ�����������ߵĽ�����ߣ���y=x2�Ľ���Ϊ��0�� ����
����
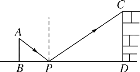
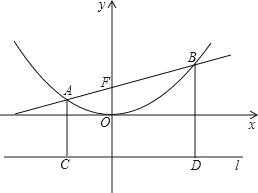
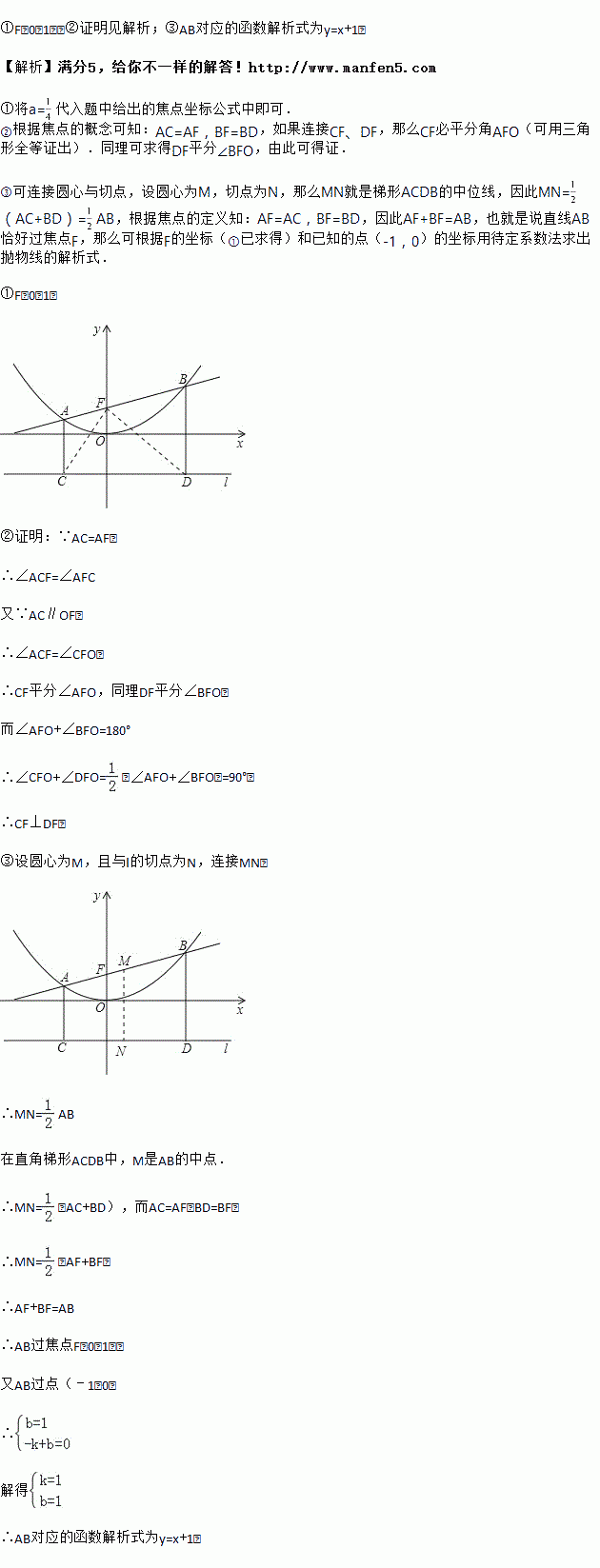
���⣺��ֱ��y=kx+b��������y= x2��A��B��AC��BD��ֱ�������ߵ���l����ֱ��ֱ�ΪC��D����ͼ����
x2��A��B��AC��BD��ֱ�������ߵ���l����ֱ��ֱ�ΪC��D����ͼ����
����������y= x2�Ľ���F�����ꣻ
x2�Ľ���F�����ꣻ
����֤��ֱ��AB������ʱ��CF��DF��
�۵�ֱ��AB���㣨��1��0���������߶�ABΪֱ����Բ����l����ʱ��������ֱ�߶�Ӧ�ĺ�������ʽ��
��ϰ��ϵ�д�
�����Ŀ

 B.
B.  C.
C. 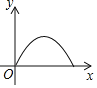 D.
D. 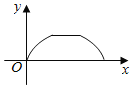
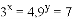 ����
���� ��ֵΪ�� ��
��ֵΪ�� �� B.
B.  C.
C.  D.
D.