题目内容
【题目】综合与探究:
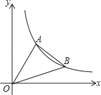
如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,其中
两点,其中![]() .
.

(1)求![]() 的值;
的值;
(2)若点![]() 是直线
是直线![]() 上的一个动点,当点
上的一个动点,当点![]() 仅在第一象限内运动时,试写出
仅在第一象限内运动时,试写出![]() 的面积
的面积![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)探索:
①在(2)条件下,当点![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积是
的面积是![]() ;
;
②在①成立的情况下,在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使△
,使△![]() 是等腰三角形?若存在,请写出满足条件的所有
是等腰三角形?若存在,请写出满足条件的所有![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
【答案】(1)k=2;(2)S=x-1;(3)①当![]() 的坐标为
的坐标为![]() 时,
时,![]() 的面积是
的面积是![]() ;②存在,点
;②存在,点![]() 坐标P1(-2
坐标P1(-2![]() ,0),P2(2
,0),P2(2![]() ,0),P3(4,0),P4(2,0)..
,0),P3(4,0),P4(2,0)..
【解析】
(1)先确定出点B的坐标,代入函数解析式中即可求出k;
(2)借助(1)得出的函数关系式,利用三角形的面积公式即可求出函数关系式;
(3)①利用三角形的面积求出求出点A坐标;
(1)∵OB=1,
∴B(1,0),
∵点B在直线y=kx-2上,
∴k-2=0,
∴k=2
(2)由(1)知,k=2,
∴直线BC解析式为y=2x-2,
∵点A(x,y)是第一象限内的直线y=2x-2上的一个动点,
∴y=2x-2(x>1),
∴S=S△AOB=![]() ×OB×|yA|=
×OB×|yA|=![]() ×1×|2x-2|=x-1,
×1×|2x-2|=x-1,
(3)①如图,
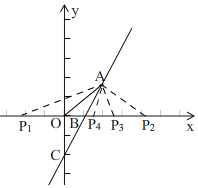
由(2)知,S=x-1,
∵△AOB的面积是1;
∴x=2,
∴A(2,2),
∴OA=2![]() ,
,
②设点P(m,0),
∵A(2,2),
∴OP=|m|,AP=![]() ,
,
①当OA=OP时,
∴2![]() =|m|,
=|m|,
∴m=±2![]() ,
,
∴P1(-2![]() ,0),P2(2
,0),P2(2![]() ,0),
,0),
②当OA=AP时,
∴2![]() =
=![]() ,
,
∴m=0或m=4,
∴P3(4,0),
③当OP=AP时,
∴|m|=![]() ,
,
∴m=2,
∴P4(2,0),
即:满足条件的所有P点的坐标为P1(-2![]() ,0),P2(2
,0),P2(2![]() ,0),P3(4,0),P4(2,0).
,0),P3(4,0),P4(2,0).

练习册系列答案
相关题目