题目内容
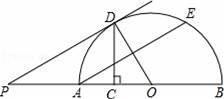
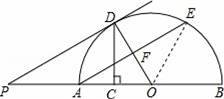
如图,AB是半圆的直径,点O是圆心,点C是OA的中点,CD⊥OA交半圆于点D,点E是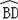
 的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.
的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.
(1)求∠AOD的度数;
(2)求证:PD是半圆O的切线.
【考点】垂径定理;平行线的性质;圆周角定理;切线的判定.
【分析】(1)根据CO与DO的数量关系,即可得出∠CDO的度数,进而求出∠AOD的度数;
(2)利用点E是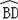
 的中点,进而求出∠EAB=30°,即可得出∠AFO=90°,即可得出答案.
的中点,进而求出∠EAB=30°,即可得出∠AFO=90°,即可得出答案.
【解答】(1)解:∵AB是半圆的直径,点O是圆心,点C是OA的中点,
∴2CO=DO,∠DCO=90°,
∴∠CDO=30°,
∴∠AOD=60°;
(2)证明:如图,连接OE,
∵点E是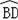
 的中点,
的中点,
∴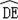
 =
=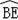
 ,
,
∵由(1)得∠AOD=60°,
∴∠DOB=120°,
∴∠BOE=60°,
∴∠EAB=30°,
∴∠AFO=90°,
∵DP∥AE,
∴PD⊥OD,
∴直线PD为⊙O的切线.



练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 ,
,  与
与 轴的正半轴的夹角为
轴的正半轴的夹角为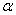 ,且
,且 ,
,
 ,若∠C=90°, ∠B=30°,BC=1,则BB′的长为( ).
,若∠C=90°, ∠B=30°,BC=1,则BB′的长为( ). C.
C. D.
D.



 中,自变量x的取值范围是
中,自变量x的取值范围是 
 ÷(a+2﹣
÷(a+2﹣
 ),其中a满足a2+3a=5.
),其中a满足a2+3a=5.
 = .
= . (B)
(B) (C)
(C) (D)
(D)