题目内容
已知多项式x3+ax2+bx+c中,a,b,c为常数,当x=1时,多项式的值是1;当x=2时,多项式的值是2;若当x是8和-5时,多项式的值分别为M与N,求M-N的值.
解:当x=1时,1+a+b+c=1,
∴a+b+c=0.①
当x=2时,8+4a+2b+c=2,
∴4a+2b+c=-6②
联立①,②解得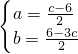 ,
,
当x=8时,M=64+64a+8b+c,
当x=5时,N=25+25a-5b+c.
∴M-N=512+64a+8b+c-(-125+25a-5b+c),
=39a+13b+637
=39×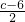 +13×
+13×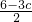 +637,
+637,
=-117+39+637,
=559.
故答案为:559.
分析:根据题意列出方程1+a+b+c=1,8+4a+2b+c=2,解得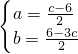 ,再由题意求出M和N的值,然后把a、b的值代入即可求出答案.
,再由题意求出M和N的值,然后把a、b的值代入即可求出答案.
点评:本题的实质是考查三元一次方程组的解法.解题的关键是消元,解题时主要运用了代入法.
∴a+b+c=0.①
当x=2时,8+4a+2b+c=2,
∴4a+2b+c=-6②
联立①,②解得
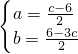 ,
,当x=8时,M=64+64a+8b+c,
当x=5时,N=25+25a-5b+c.
∴M-N=512+64a+8b+c-(-125+25a-5b+c),
=39a+13b+637
=39×
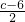 +13×
+13×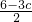 +637,
+637,=-117+39+637,
=559.
故答案为:559.
分析:根据题意列出方程1+a+b+c=1,8+4a+2b+c=2,解得
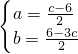 ,再由题意求出M和N的值,然后把a、b的值代入即可求出答案.
,再由题意求出M和N的值,然后把a、b的值代入即可求出答案.点评:本题的实质是考查三元一次方程组的解法.解题的关键是消元,解题时主要运用了代入法.

练习册系列答案
相关题目
已知多项式x2+ax+b与x2-2x-3的乘积中不含x3与x2项,则a,b的值为( )
| A、a=2,b=7 | B、a=-2,b=-3 | C、a=3,b=7 | D、a=3,b=4 |