题目内容
【题目】(如图(1),在矩形ABCD中,AB=4,BC=3,点E是射线CD上的一个动点,把△BCE沿BE折叠,点C的对应点为F.
(1)若点F刚好落在线段AD的垂直平分线上时,求线段CE的长;
(2)若点F刚好落在线段AB的垂直平分线上时,求线段CE的长;
(3)当射线AF交线段CD于点G时,请直接写出CG的最大值 .


【答案】(1)CE=![]() ;(2)CE=
;(2)CE=![]() ;(3)CG的最大值是4-
;(3)CG的最大值是4-![]()
【解析】(1)根据垂直平分线的性质,等边三角形的性质求出即可;(2)利用垂直平分线的性质得出FE=EC ,再利用相似三角形的性质进而得出答案;(3)当射线AF交线段CD于点G时求出即可.
解: ∵点F刚好落在线段AD的垂直平分线上,∴FB=FC.
∵折叠 ,∴FB=BC=3.
∴△FBC是等边三角形,∴∠FBC=60°, ∠EBC=30°.
在Rt△EBC,∴CE=![]() BC=
BC=![]() .
.
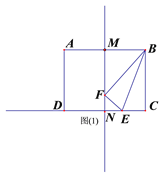
(2)如图(1)∵点F刚好落在线段AB的垂直平分线MN上,
∵折叠,∴FE=EC.
∴BM=2,在Rt△MFB中,MF=![]() .
.
∵△MBF∽△NFE,
∴![]() =
=![]() .
.
∴CE=EN=![]() .
.
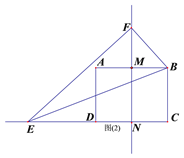
如图(2)∵折叠 ,∴FE=EC.
同理MF=![]() ,FN=3+
,FN=3+![]() .
.
∵△MBF∽△NFE,∴![]() =
=![]() .
.
∴CE=EN=![]() .
.
(3)CG的最大值是4-![]() .
.
“点睛”此题主要考查了垂直平分线、等边三角形、矩形的性质、翻折变换的性质、相似三角形等知识;利用数形结合以及分类讨论得出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目