题目内容
一元二次方程5（x+3）=（x+3）2的根是
- A.x=5
- B.x=-3
- C.x1=-3，x2=-2
- D.x1=-3，x2=2
D
分析：移项后分解因式得出（x+3）（2-x）=0，推出x+3=0，2-x=0，求出方程的解即可．
解答：移项得：5（x+3）-（x+3）2=0，
（x+3）[5-（x+3）]=0，
（x+3）（2-x）=0，
x+3=0，2-x=0，
解得：x1=-3，x2=2，
故选D．
点评：本题考查了解一元二次方程，解此题的关键是把一元二次方程转化成解一元一次方程，题目比较典型，是一道比较好的题目．
分析：移项后分解因式得出（x+3）（2-x）=0，推出x+3=0，2-x=0，求出方程的解即可．
解答：移项得：5（x+3）-（x+3）2=0，
（x+3）[5-（x+3）]=0，
（x+3）（2-x）=0，
x+3=0，2-x=0，
解得：x1=-3，x2=2，
故选D．
点评：本题考查了解一元二次方程，解此题的关键是把一元二次方程转化成解一元一次方程，题目比较典型，是一道比较好的题目．
练习册系列答案
相关题目
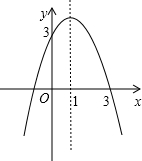已知二次函数y=-x2+bx+c的图象如图所示，解决下列问题：
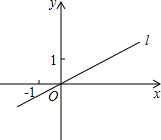如图，在平面直角坐标系中，直线l的解析式为y=