题目内容
(本题满分12分)如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A,B两点,开口向下的抛物线经过点A,B,且其顶点P在⊙C上.
(1)求∠ACB的大小;
(2)写出A,B两点的坐标;
(3)试确定此抛物线的解析式;
(4)在该抛物线上是否存在一点D,使线段OP与CD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.
(1)120°
(2)A(1- ,0 ) B(1+
,0 ) B(1+ ,0)
,0)
(3)
(4)点D在抛物线上 所以存在D(0,2)使线段OP与CD互相平分
解析试题分析:(1)
解:过点作CM⊥AB,得CM=1,
∵AC=2,∴∠CAB=30°,∴∠ACB=120° (2分)
(2)∵CM=1,AC=2,∴AM=
∴A(1- ,0 ) B(1+
,0 ) B(1+ ,0) (2分)
,0) (2分)
(3)
解:由题可得该抛物线的对称轴为 直线x=1,PM=3
∴顶点坐标为(1,3) (1分)
设
经过点A(1- ,0 ) ,得 0=3a+3
,0 ) ,得 0=3a+3
∴a=-1 ∴ (2分)
(2分)
(4)解:存在 (1分)
假设存在点D使线段OP与CD互相平分,则四边形OCPD是平行四边形
∴PC//OD且PC=OD.
∵PC//y轴,∴点D在y轴上.
又∵PC=2,∴OD=2,即D(0,2). (2分)
又D(0,2)满足
∴点D在抛物线上 所以存在D(0,2)使线段OP与CD互相平分. (2分)
考点:本题考查了待定系数法求解二次函数
点评:此类试题属于难度较大的试题,考生在解答此类试题时一定要对待定系数法解二次函数的基本知识熟练把握

(本题满分12分)
如图, 的顶点A、B在二次函数
的顶点A、B在二次函数 的图像上,又点A、B[来分别在
的图像上,又点A、B[来分别在 轴和
轴和 轴上,
轴上, ∠ABO=
∠ABO= .
.

1.(1)求此二次函数的解析式;(4分)
2.
|
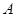 作
作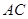 ∥
∥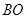 交上述函数图像于点
交上述函数图像于点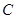 ,
,
点 在上述函数图像上,当
在上述函数图像上,当 与
与 相似时,求点
相似时,求点 的坐标.(8分)
的坐标.(8分)

 的长;
的长;
 与x轴交于A、C两点,与y轴交于B点,与直线
与x轴交于A、C两点,与y轴交于B点,与直线 交于A、D两点。
交于A、D两点。 落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?
落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?

 ,
, ,
, .动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
 时,求线段
时,求线段 的长;
的长; 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由.